TO THE EDITOR:
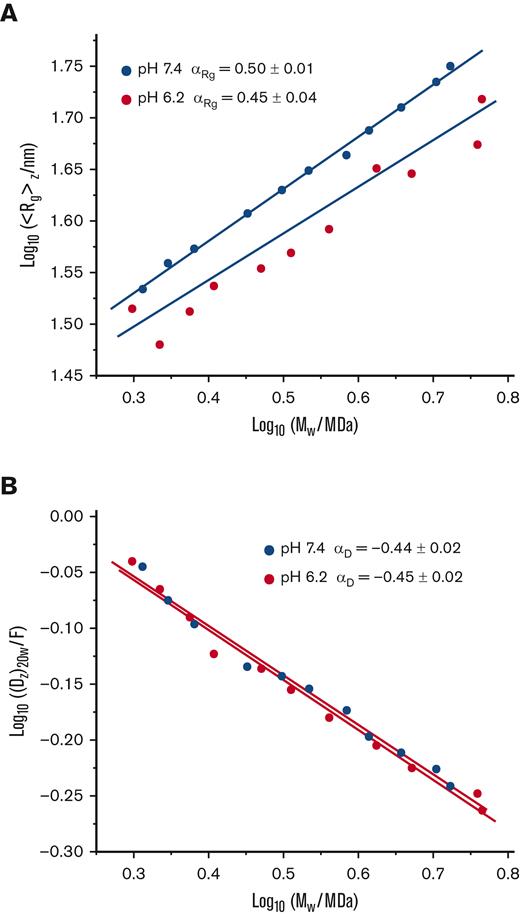
von Willebrand factor (VWF) is a multimeric plasma glycoprotein necessary for normal vertebrate hemostasis. It is a linear homopolymer consisting of a variable number of concatenated ∼280 kDa subunits.1 The conformation of VWF multimers has been controversial. The spectrum of macromolecular conformations ranges from a globular particle to a random coil to a rod-like particle2 (p. 261). Based on electron microscopy, atomic force microscopy, small-angle neutron scattering, total internal reflection fluorescence microscopy, and theoretical studies, the conformation of multimeric VWF under static conditions has been variably described as a “ball-of-yarn,”3 a “tangled coil,”4 a “compact, bird’s nest,”1 a “compact fuzz ball,”5 “compact and globular,”6 and a “dense globule.”7 These descriptions suggest that the conformation of VWF is a function of strong attractive forces between subunits.8 However, recently the characterization of VWF at pH 7.4 by sedimentation velocity analytical ultracentrifugation, dynamic light scattering (DLS), and multiangle light scattering (MALS) have challenged this notion.9,10 Conformation plots of the sedimentation coefficient, diffusion coefficient, and radius of gyration as a function of molecular weight were consistent with a random coil conformation and not a folded, globular conformation.
The characterization of the conformation of VWF at pH 6.2 of the trans-Golgi where multimerization occurs is an additional physiologically relevant problem. In the present study, we fractionated VWF/fVIII complexes by size-exclusion chromatography (SEC) at either pH 6.2 or pH 7.4 across a molecular weight range of ∼2 to 6 MDa and measured the ratio of the radius of gyration to the hydrodynamic radius. Our results are consistent with a random coil conformation at both pH 6.2 and pH 7.4.
VWF/fVIII complexes in Alphanate (antihemophilic factor/VWF complex [human], Grifols USA), a commercial product used in the treatment of von Willebrand disease and hemophilia A,11,12 were fractionated by SEC at pH 6.2 and pH 7.4, studied by MALS to obtain estimates of molecular weight and radius of gyration, and by DLS to obtain estimates of the diffusion coefficient and hydrodynamic radius. Material from 2 vials of Alphanate were dissolved by adding 10 mL of sterile water for injection to each vial. The sample was applied to a 2.5 × 120 cm Sephacryl S-1000 SEC column equilibrated in 0.15 M sodium chloride, 0.02 M N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (HEPES), 5 mM calcium chloride (HEPES-buffered saline [HBS]/calcium [Ca] buffer) at pH 6.2 or pH 7.4 at room temperature at a flow rate of 0.3 mL/min. VWF/fVIII complexes emerged as a single peak and contained at least 95% VWF as judged by reduced sodium dodecyl sulfate–polyacrylamide gel electrophoresis. Fractions containing VWF/fVIII complexes were diluted to 0.15 mg/mL in HBS/Ca buffer and frozen in 0.45-mL aliquots at −80 °C.
SEC MALS was performed on SEC-fractionated VWF/fVIII complexes using a DAWN MALS detector and Optilab differential refractometer (Wyatt Corporation) in line with a 1260 Infinity II high performance liquid chromatography system (Agilent Corporation) and a Superdex 200 10/300 GL SEC column (GE Healthcare Life Sciences) in HBS/Ca at pH 6.2 or pH 7.4, as described previously.10 Data acquisition and analysis were performed using ASTRA version 8.1.1.12 (Wyatt Corporation). VWF/fVIII complexes eluted as a single peak near the void volume. Estimates of the weight-average molecular weight (Mw) and the z-average radius of gyration of the VWF/fVIII peak were made using the Berry model.13,14
Conformation plots of SEC-fractionated VWF/fVIII complexes. VWF/fVIII complexes fractionated by Sephacryl S-1000 SEC at pH 6.2 or pH 7.4 were analyzed by SEC MALS to obtain estimates of the weight-average molecular weight and radius of gyration, and by DLS to obtain estimates of the z-average diffusion coefficient. The results are plotted as log10 ⟨Rg⟩z vs log10 Mw (A) or log10 (Dz)20w vs log10 Mw (B). The units of Dz are Ficks (1 F = 10−7 cm2/s). Further shown are the fitted simple linear regression lines and Mark-Houwink-Kuhn-Sakurada exponents with standard errors obtained from the slopes of the regression lines calculated using Prism (version 9.3.0).
Conformation plots of SEC-fractionated VWF/fVIII complexes. VWF/fVIII complexes fractionated by Sephacryl S-1000 SEC at pH 6.2 or pH 7.4 were analyzed by SEC MALS to obtain estimates of the weight-average molecular weight and radius of gyration, and by DLS to obtain estimates of the z-average diffusion coefficient. The results are plotted as log10 ⟨Rg⟩z vs log10 Mw (A) or log10 (Dz)20w vs log10 Mw (B). The units of Dz are Ficks (1 F = 10−7 cm2/s). Further shown are the fitted simple linear regression lines and Mark-Houwink-Kuhn-Sakurada exponents with standard errors obtained from the slopes of the regression lines calculated using Prism (version 9.3.0).
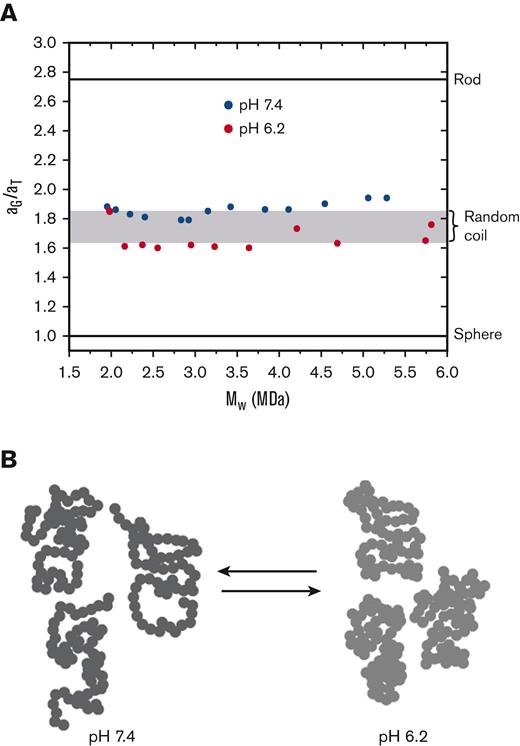
Additional information can be obtained from the ratios of equivalent radii associated with measurement of the diffusion coefficient and radius of gyration.20,21 An equivalent radius is the radius of a spherical particle having the same value of the solution property as that of the macromolecule under consideration. Figure 2A shows plots of the aG/aT ratio as a function of the molecular weight of VWF at pH 6.2 and pH 7.4. The values are independent of molecular weight, cluster around those expected for a random coil, and are distinctly higher than the value of 1 for a spherical (globular) molecule. The values at pH 6.2 are lower than those at pH 7.4. This difference is because of a decrease in the radius of gyration (Figure 1A), which is a measure of the distance of the mass elements of a macromolecule from its center of mass. These results are consistent with negative stain electron microscopy by Zhou et al showing self-association of VWF domains into dimeric “bouquets.”5
Ratios of equivalent radii(aG/aT) of SEC-fractionated VWF/fVIII complexes. (A) The equivalent radii, aG and aT, of VWF/fVIII fractionated at pH 6.2 or pH 7.4 by Sephacryl S-1000 SEC were calculated using the values of ⟨Rg⟩z and (Dz)20w using equations 1 and 2. The dimensionless ratio (aG/aT) is plotted vs estimates of Mw obtained by MALS. The horizontal lines corresponding to aG/aT ratios for spheres and rods were calculated as described.20 The shaded region corresponds to the range of aG/aT ratios expected for a random coil, in which upper and lower limits represent the presence and absence of excluded volume, respectively.20 (B) Cartoon of a pearl string random coil polymer. The more localized distribution of mass for the conformations on the right corresponds to a decreased radius of gyration at pH 6.2.
Ratios of equivalent radii(aG/aT) of SEC-fractionated VWF/fVIII complexes. (A) The equivalent radii, aG and aT, of VWF/fVIII fractionated at pH 6.2 or pH 7.4 by Sephacryl S-1000 SEC were calculated using the values of ⟨Rg⟩z and (Dz)20w using equations 1 and 2. The dimensionless ratio (aG/aT) is plotted vs estimates of Mw obtained by MALS. The horizontal lines corresponding to aG/aT ratios for spheres and rods were calculated as described.20 The shaded region corresponds to the range of aG/aT ratios expected for a random coil, in which upper and lower limits represent the presence and absence of excluded volume, respectively.20 (B) Cartoon of a pearl string random coil polymer. The more localized distribution of mass for the conformations on the right corresponds to a decreased radius of gyration at pH 6.2.
A crude representation of the solution conformation of VWF is depicted in Figure 2B using the classical pearl string model of random coil polymer22 (p. 602). Only 3 conformations from a vast number of available conformations are shown. The polymer contains 60 beads, which, at 30 kDa per bead, would correspond to a 1.8 MDa VWF multimer. The polymer at pH 6.2 is shown pervading less space than at pH 7.4, corresponding to a smaller radius of gyration.
Our finding that VWF displays random coil behavior at its biologically relevant pH values of 6.2 and 7.4 has important implications with respect to the biosynthesis and function of VWF. Pro-VWF dimers are transported from the endoplasmic reticulum to the trans-Golgi, where the VWF propeptide is cleaved and multimerization occurs.23 The propeptide/multimer complex remains noncovalently associated and aggregates into tubules that form nascent Weibel–Palade bodies. Exocytosis of Weibel–Palade bodies produces VWF “strings” that are extruded into plasma. The random coil conformation of VWF, in contrast to a compact, globular conformation, may be necessary for VWF to feed into a tubule and become extruded from a Weibel–Palade body. The smaller radius of gyration observed at pH 6.2 may facilitate assembly of the VWF random coil into Weibel–Palade bodies. It has been proposed that the activation of VWF in plasma at pH 7.4 by shear stress under flow includes unraveling a compact, globular VWF conformation.1,8 A random coil conformation obviates the need for that hypothesis.
Acknowledgments: This work was supported by awards from the National Heart, Lung and Blood Institute, National Institutes of Health (U54HL141981) (P.L.) and the American Society of Hematology Medical Student Physician-Scientist Award (I.W.S.).
Contribution: All authors designed and performed research, analyzed data, and cowrote the manuscript.
Conflict-of-interest disclosure: P.L. is an inventor on patents claiming compositions of matter that include modified fVIII proteins.
Correspondence: Pete Lollar, Department of Pediatrics, Room 438, Emory Children's Center Emory University, 2015 Uppergate Dr, Atlanta, GA 30322; e-mail: jlollar@emory.edu.
References
Author notes
Data are available on request from corresponding author, Pete Lollar (jlollar@emory.edu).