The binding of plasma von Willebrand factor (VWF) to platelet receptor GpIb under high hydrodynamic shear leads to platelet activation and subsequent shear-induced platelet aggregation (SIPA). We quantitatively examined the aspects of fluid flow that regulate platelet activation by subjecting human blood and isolated platelets to well-defined shear conditions in a cone-plate viscometer. We made the following observations. First, Annexin V binding to phosphatidyl serine expressed on activated cells was detectable within 10 seconds of shear application. Second, fluid shear stress rather than shear rate controls platelet activation, and a threshold shear stress of approximately 80 dyn/cm2 is necessary to induce significant activation. Under these conditions, individual domains of soluble VWF and platelet GpIb are subjected to similar magnitudes of fluid forces on the order of 0.1 pN, whereas GpIb with bound VWF is subjected to 1 pN. Third, cell-cell collisions and time-varying stresses are not essential for platelet activation. Fourth, the mechanism of platelet activation can be resolved in 2 steps based on the contribution of VWF and fluid forces. Fluid shear and VWF are required during the first step, when GpIb-VWF binding likely occurs. Subsequently, high shear forces alone in the absence of VWF in suspension can induce platelet activation. In other experiments, purified VWF was subjected to shear in the viscometer, and VWF morphology was assessed using light scattering. These studies demonstrate, for the first time, the ability of hydrodynamic forces to induce VWF aggregation in suspension. This VWF self-association may be an additional feature involved in controlling cell adhesion rates in circulation.
Introduction
High fluid shear may trigger the activation of platelets and their subsequent aggregation.1-4 This process is termed shear-induced platelet aggregation (SIPA). The molecular mechanism involves the shear-induced binding of von Willebrand factor (VWF) to the platelet membrane GpIb/IX/V complex.5,6 This binding initiates signaling events that lead to increased intracellular calcium levels7-9 and to platelet GpIIb-IIIa receptor activation. Platelet-platelet aggregates are subsequently formed as a result of the bridging of GpIIb-IIIa on adjacent platelets by VWF. It has been suggested that SIPA may play a role in the pathogenesis of vascular diseases because platelets from patients with acute myocardial infarction10,11 and cerebral ischemia12 13 display enhanced SIPA in vitro.
In the current manuscript, we examine the features of fluid flow that regulate shear-induced platelet activation (SIPAct). We prefer to use Annexin V binding to platelets as a marker of cell activation because this is an early and quantitative indicator. Following platelet activation, the translocation of phosphatidyl serine (PS) from the inner leaflet of the platelet plasma membrane to the platelet surface occurs rapidly. This contributes to the procoagulant activity of the cells. The exact mechanism of PS transmembrane redistribution is unknown, but it is established that this is one of the early markers of cells undergoing apoptosis14,15 and of platelets undergoing activation.16-18 Annexin V is a placental anticoagulant protein that binds PS with high affinity; thus, it reports on platelet activation levels.19,20 Resting platelets express approximately 5000 PS molecules on their surfaces, and activation induces up to a 40-fold increase in PS expression.21 Other methods we used to assay platelet activation, including microparticle formation and cell aggregation measurements, were not as quantitative. For example, though SIPA reports on GpIb-VWF binding, it is also a complex function of many factors including the expression of activated GpIIb-IIIa, the rate of cell-cell collisions, and the probability of stable aggregate formation following collision.22 In addition, though measurement of VWF binding to platelets has been used to quantify SIPAct, this assay may report on VWF binding to both GpIb and GpIIb/IIIa.1Thus, it may fail to capture transient VWF-GpIb interactions that contribute to platelet activation.
In this paper, we demonstrate that fluid shear stress, not shear rate, plays an active role in initiating SIPAct. This activation does not require the occurrence of cell-cell collisions or the application of time-varying shear stress. Further, we propose a 2-step model of SIPAct based on the contributions of VWF and fluid forces. Although several studies have reported on selected aspects of hydrodynamic flow that contribute to platelet activation, to the best of our knowledge, this is the first study to systematically examine all the features and to report on the predominant role of shear stress. In another set of experiments, we used light scattering to assess VWF morphology in suspension and to study the macroscopic alterations in protein structure in response to hydrodynamic shear. These experiments reveal that fluid forces may induce homotypic adhesion between soluble VWF molecules. Recently, another study has proposed that the self-association of VWF may contribute to platelet deposition in a model of vascular injury.23 Our results suggest that VWF self-association may be shear mediated.
Materials and methods
Materials
CD61-Per CP was purchased from Becton Dickinson (San Jose, CA), Annexin V–fluorescein isothiocyanate (FITC) from Molecular Probes (Eugene, OR), polyclonal rabbit antihuman VWF and GpIb function blocking antibody AN-51 (IgG2a) from DAKO-USA (Carpinteria, CA), and polyclonal mouse antihuman fibrinogen from Nordic Immunological (Turnhout, Belgium). GpIIb-IIIa function blocking antibody BLE-6 (IgG1) was from Sigma (St Louis, MO), 7E3 (IgG1) was provided by Dr J. Balthasar (SUNY-Buffalo, NY), and recombinant VWF A1 domain24 was provided by Dr Miguel Cruz (Baylor College of Medicine, Houston, TX). Secondary horseradish peroxidase–conjugated goat antirabbit and goat antimouse antibodies were from Jackson Immunoresearch (West Grove, PA). Sepharose 4B was purchased from Amersham Pharmacia (Piscataway, NJ).
Platelet isolation
Platelets were isolated from blood obtained from healthy nonsmoking human volunteers, as described earlier.25Briefly, blood was drawn either in 100 μM d-Phe-Pro-Arg-chloromethyl ketone (PPACK; Bachem, King of Prussia, PA) or in 10% vol/vol 3.8% sodium citrate. Blood was centrifuged at 150gfor 12 minutes to obtain platelet-rich plasma (PRP) from supernatant. Remaining blood was further spun at 500g for 20 minutes to obtain platelet-poor plasma (PPP). Platelet concentration was determined using a Coulter Counter (Fullerton, CA). Platelets were stored at room temperature and were used within 2 hours of isolation.
Shear stress in the cone-plate viscometer
Cell activation was induced by shearing platelets in a cone-plate viscometer (model VT550; Haake, Paramus, NJ). This viscometer consists of a stationary plate surface placed directly beneath a rotating 0.5° cone. This device allows the application of well-defined fluid shear on cells in suspension.26 27 At low cone rotation rates, the shear rate in the viscometer is constant throughout the device. This flow is termed primary flow. This is equivalent to a linear shear field, in which the fluid velocity increases in proportion to the distance from the plate. In a viscometer with cone angle α rotated at a constant angular velocity Ω, the applied shear rate G during primary flow is given by G = Ω/tanα.
When the cone rotation or sample volume is increased, along with fluid circulation in the direction of cone rotation, centrifugal forces at the cone surface cause additional fluid flow in the radial direction.28 This flow pattern is called secondary flow, and it occurs under shear conditions applied in conventional SIPA studies.26 27 Secondary flow causes spatial variations in local shear rate. Platelets and soluble plasma proteins circulating in the viscometer are thus exposed to varying levels of shear, depending on their location. This results in the application of time-varying stresses on cells and soluble molecules. Supplemental material on theBlood website describes methods to estimate the distribution of shear rate and the magnitude of time-varying shear applied in the viscometer; see the Supplemental Document link at the top of the online article.
An important feature of secondary flow is that by increasing the sample volume at any given cone rotation rate, time-varying stresses can be enhanced without altering the average shear stress applied. Thus, to examine the effects of time-varying stress in the current paper, we compared SIPAct in runs with 2 different sample volumes: 55 μL and 300 μL.
The shear stress τ for Newtonian fluids is directly proportional to the shear rate according to τ = μG, where μ is the media viscosity. In some runs, to distinguish between the contributions of shear rate and shear stress, media viscosity was altered by the addition of dextran (MWt 2 × 106) dissolved in HEPES buffer29 to a final concentration of 1.5% wt/vol. For these runs, appropriate controls were performed through the addition of HEPES (N-2-hydroxyethylpiperazine-N'-2-ethanesulfonic acid) buffer to the PRP-PPP mixture. Media viscosity was measured using a Cannon-Fenske capillary viscometer (Cannon Instruments, State College, PA).
Shear-induced platelet activation
PRP was supplemented with PPP in either the presence or absence of blocking antibodies to obtain concentrations between 10 × 106 and 300 × 106 platelets/mL. Cells were incubated at room temperature for 5 minutes and then at 37°C for 3 minutes. In most experiments, the volume of the platelet suspension was 100 μL. Exceptions to this were studies that examined the role of time-varying stress, where the volume was either 55 μL or 300 μL. Platelet samples were sheared in the cone-plate viscometer at 37°C. Some shear runs were similarly performed for citrated whole blood. At specific time points, samples were drawn and platelets at a concentration of 5 × 106/mL were incubated with 1:5 CD61-PerCP and 1:20 Annexin V–FITC in HEPES containing 5 mM Ca2+ for 5 minutes at 37°C. Samples were then read in a FACScalibur flow cytometer (Becton Dickinson). Fluorescence from CD61-PerCP was used as a marker of platelets and platelet-derived microparticles. Single platelets and microparticles were distinguished based on their characteristic forward versus side scatter. We measured the FITC fluorescence of a small population of single platelets to monitor Annexin V binding. Percentage activation was quantified as the fraction of platelets that displayed greater than baseline levels of Annexin V binding. Control experiments in which Annexin V–FITC was added to platelets before shear illustrated that the post-shear incubation protocol described here reflects the true activation levels of platelets at the time of shear stoppage (data not shown). Microparticle formation was quantified by monitoring the percentage increase in microparticle number compared with baseline (t = 0).
Purification of VWF
VWF was purified from human plasma cryoprecipitate obtained from the American Red Cross (Buffalo, NY), as described earlier30 31 except for the final chromatography step. Here, the VWF-enriched solution was applied to a Sepharose 4B column (0.7 × 50 cm) and was eluted with HEPES buffer at a flow rate of 5 mL/h using FPLC (Pharmacia). Fractions of approximately 1 mL were collected. Purified VWF typically eluted near the void volume. Fractions 1 to 4 were pooled for viscometry and light-scattering experiments. Protein concentrations were measured using Bradford dye-binding (Bio-Rad, Hercules, CA). Western blotting (detailed immediately below) was used to verify the presence of VWF and the absence of fibrinogen in the preparations. Human plasma was used as a positive control.
Western blotting
Western blot analysis of VWF was performed as described elsewhere.32 In the final step, membranes were developed using the chemiluminescence LUMIGLO peroxidase kit (KPL, Gaithersburg, MD) for 1 minute and were imaged onto Kodak Biomax ML film (Eastman-Kodak, Rochester, NY). Exposure times varied from 30 seconds to 3 minutes. The film was photographed using a digital camera, and densitometry was performed using Kodak-1D software.
Static and dynamic light scattering of VWF
Purified VWF samples that were unsheared or were subjected to shear were analyzed using light scattering. In each run, the sample was placed in the borosilicate glass cuvette of a Brookhaven Goniometer (BI-200SM Ver.2.0; Brookhaven Instruments, Holtsville, NY) maintained at 37°C. Samples were exposed to 514 nm laser light, and the intensity of scattered light was measured at various angles with respect to the incident beam. Light intensity was measured in terms of the photon count rate using a photon counter.
Two types of light-scattering measurements were performed to quantify VWF shape and size. Static light scattering (SLS) was used to determine the molecular weight (MWt) and radius of gyration (Rg) of the protein. For this analysis, the photon count rate was collected at detector angles (θ) varying from 35° to 145° with respect to the incident beam. Data were used to calculate the Rayleigh ratio,RA(θ), as discussed in the supplemental online document. A Zimm plot was generated by plottingKCA/RA(θ) against sin2(θ/2) + αCA, where K is an instrument constant, CAis the VWF concentration, and α is a parameter derived from the curve-fitting software. Extrapolation of the data toCA = 0 allowed the estimation of MWt andRg. Dynamic light scattering (DLS) was used to estimate the hydrodynamic radius (Rh). Here, the photon count rate was measured at a fixed angle perpendicular to the incident light (θ = 90°). An auto-correlator (BI-9000AT; Brookhaven Instruments) analyzed these data to estimate protein diffusivity. This diffusivity was then converted to estimate the hydrodynamic radius (Rh). The detailed theory and calculation scheme is described in the supplemental online document and elsewhere.33 34
Following an initial set of trial runs, a rigorous methodology was established for light scattering data collection. Purified VWF used for light scattering was isolated within 1 to 3 days before the experiment and was centrifuged at 40 000g for 1 hour on the day of the experiment to remove any protein aggregates. In runs with the unsheared sample, VWF samples at various concentrations from 0.0045 to 0.045 mg/mL were examined. In the sheared runs, 125 μL VWF at approximately 0.1 mg/mL was sheared in the cone-plate viscometer, and the samples were immediately diluted 1:8 in HEPES buffer for analysis. SLS assay was performed immediately after shear was stopped. Typically, an approximately 30-second delay occurred between the stoppage of shear and the acquisition of the first data point. In addition, it typically took approximately 3 minutes to acquire SLS data over the range of angles. In some runs, 0.1% sodium dodecyl sulfate (SDS) was added to sheared or unsheared samples immediately after they were analyzed using SLS. Samples were then reanalyzed to examine the effect of SDS addition. Sheared samples were analyzed using SLS approximately every hour up to 5 hours after the stoppage of shear. SLS and DLS analyses were performed at this 5-hour time point. The time taken for DLS analysis was approximately 30 seconds. The protein concentration of all sheared samples was also measured using the Bio-Rad protein assay to quantify the loss of VWF to the viscometer surface. This information was used for SLS and for Western blot analysis.
Statistics
Statistical significance was determined using paired Student t test or analysis of variance (ANOVA).P < .05 was considered significant.
Results
We examined various aspects of SIPAct using Annexin V to quantify platelet activation and light scattering and Western blot analyses to assess shear-dependent changes in VWF morphology and multimer distribution. To remain consistent with other reports in the SIPA/SIPAct literature, the shear rate provided here is based on the linear flow assumption. All SIPAct results (Figures1-5), with the exception of Figure 5A, are presented for PPP and PRP isolated from sodium citrate anticoagulated blood. As noted below, runs using PPACK anticoagulated blood yielded similar results.
Detection of platelet activation.
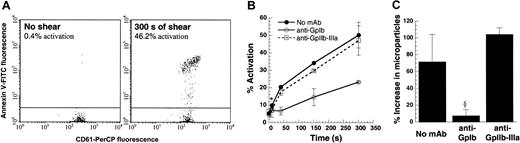
One hundred microliters platelets at 10 × 106 cells/mL in citrated PPP were sheared at 9600/s in a cone-plate viscometer with a 0.5° cone for 300 seconds. Function-blocking antibodies against GpIb (AN-51) and GpIIb-IIIa (BLE-6 or 7E3) were added in some runs. CD61-PerCP fluorescence was used to gate on platelets and microparticles. (A) Flow cytometric detection of activated platelets using Annexin V–FITC at t = 0 and 300 seconds. (B) SIPAct as a function of shearing time in the absence or presence of antibodies. Significant binding was observed at the earliest sampling time point, 10 seconds. (C) Percentage increase in microparticle number at t = 300 seconds after shear compared with the number at t = 0. Data are mean ± SEM for n ≥ 3. *P < .05 with respect to t = 0 sample. §P < .05 with respect to anti–GpIIb-IIIa treatment.
Detection of platelet activation.
One hundred microliters platelets at 10 × 106 cells/mL in citrated PPP were sheared at 9600/s in a cone-plate viscometer with a 0.5° cone for 300 seconds. Function-blocking antibodies against GpIb (AN-51) and GpIIb-IIIa (BLE-6 or 7E3) were added in some runs. CD61-PerCP fluorescence was used to gate on platelets and microparticles. (A) Flow cytometric detection of activated platelets using Annexin V–FITC at t = 0 and 300 seconds. (B) SIPAct as a function of shearing time in the absence or presence of antibodies. Significant binding was observed at the earliest sampling time point, 10 seconds. (C) Percentage increase in microparticle number at t = 300 seconds after shear compared with the number at t = 0. Data are mean ± SEM for n ≥ 3. *P < .05 with respect to t = 0 sample. §P < .05 with respect to anti–GpIIb-IIIa treatment.
Effect of cell collision on platelet activation.
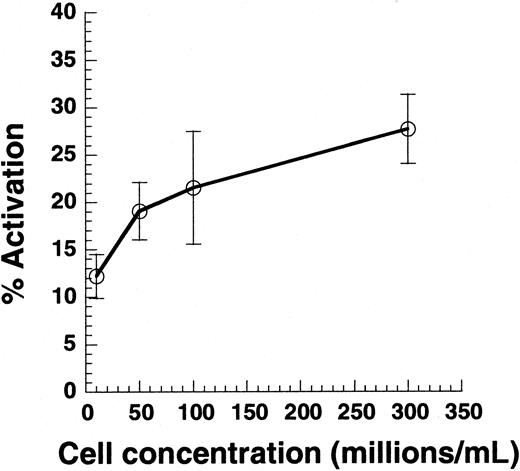
Citrated PRP was diluted in PPP to achieve platelet concentrations between 10 × 106 and 300 × 106 cells/mL. Cell suspension (100 μL) was subjected to shear in a cone-plate viscometer at 9600/s. Twenty-second samples were analyzed for Annexin V–FITC binding. Data are mean ± SEM for n = 4-7.
Effect of cell collision on platelet activation.
Citrated PRP was diluted in PPP to achieve platelet concentrations between 10 × 106 and 300 × 106 cells/mL. Cell suspension (100 μL) was subjected to shear in a cone-plate viscometer at 9600/s. Twenty-second samples were analyzed for Annexin V–FITC binding. Data are mean ± SEM for n = 4-7.
Shear rate versus shear stress.
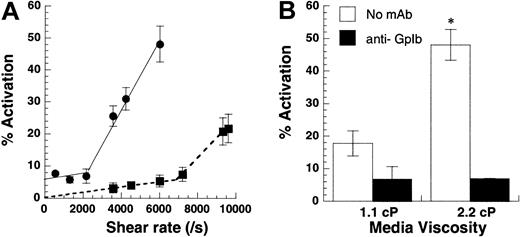
(A) Shear-induced platelet activation in undiluted citrated whole blood (●) was compared with citrated PRP with platelets at 10 × 106 cells/mL (▪). Platelet activation levels assayed using Annexin V–FITC are reported at 180 seconds for whole blood runs and at 30 seconds for citrated PRP. Lower shear rates of 2200/s (shear stress, approximately 83 dyn/cm2) were required for platelet activation in whole blood compared with 6800/s (shear stress, approximately 75 dyn/cm2) for platelets in PRP. The threshold shear stress requirement was comparable for both treatments. (B) Media viscosity was doubled by the addition of 1.5% wt/vol dextran, and the effect of increasing media viscosity on isolated platelets at 10 × 106 cells/mL was examined at 9600/s after 30 seconds of shear. GpIb blocking antibody AN-51 reduced platelet activation levels to baseline values in the presence and in the absence of dextran. Data are mean ± SEM for n = 3-4. *P < .05 with respect to run, without the addition of dextran.
Shear rate versus shear stress.
(A) Shear-induced platelet activation in undiluted citrated whole blood (●) was compared with citrated PRP with platelets at 10 × 106 cells/mL (▪). Platelet activation levels assayed using Annexin V–FITC are reported at 180 seconds for whole blood runs and at 30 seconds for citrated PRP. Lower shear rates of 2200/s (shear stress, approximately 83 dyn/cm2) were required for platelet activation in whole blood compared with 6800/s (shear stress, approximately 75 dyn/cm2) for platelets in PRP. The threshold shear stress requirement was comparable for both treatments. (B) Media viscosity was doubled by the addition of 1.5% wt/vol dextran, and the effect of increasing media viscosity on isolated platelets at 10 × 106 cells/mL was examined at 9600/s after 30 seconds of shear. GpIb blocking antibody AN-51 reduced platelet activation levels to baseline values in the presence and in the absence of dextran. Data are mean ± SEM for n = 3-4. *P < .05 with respect to run, without the addition of dextran.
Effect of time-varying stress on platelet activation.
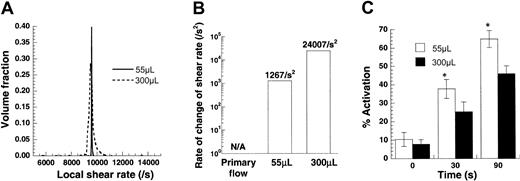
Platelets (100 × 106/mL) from citrated blood were sheared in a cone-plate viscometer at 9600/s. Sample volumes were either 55 μL or 300 μL. Numerical analyses of this experiment are presented in panels A and B, and experimental data are depicted in panel C. (A) Distribution of local shear rates in the viscometer for the 2 sample volumes calculated based on numerical solution of the flow in this device. The average shear rate in each experiment is the same (approximately 9600/s), though the deviation from the mean is higher for the larger sample volume. (B) Mean rate of change of shear rate applied on a circulating cell/molecule is presented for the 2 sample volumes. Time-varying shear stresses are approximately 19 times greater for the larger sample volumes. (C) Increasing sample volume decreased platelet activation by approximately 30%. Data are mean ± SEM for n = 6. *P < .05 with respect to a 300 μL run.
Effect of time-varying stress on platelet activation.
Platelets (100 × 106/mL) from citrated blood were sheared in a cone-plate viscometer at 9600/s. Sample volumes were either 55 μL or 300 μL. Numerical analyses of this experiment are presented in panels A and B, and experimental data are depicted in panel C. (A) Distribution of local shear rates in the viscometer for the 2 sample volumes calculated based on numerical solution of the flow in this device. The average shear rate in each experiment is the same (approximately 9600/s), though the deviation from the mean is higher for the larger sample volume. (B) Mean rate of change of shear rate applied on a circulating cell/molecule is presented for the 2 sample volumes. Time-varying shear stresses are approximately 19 times greater for the larger sample volumes. (C) Increasing sample volume decreased platelet activation by approximately 30%. Data are mean ± SEM for n = 6. *P < .05 with respect to a 300 μL run.
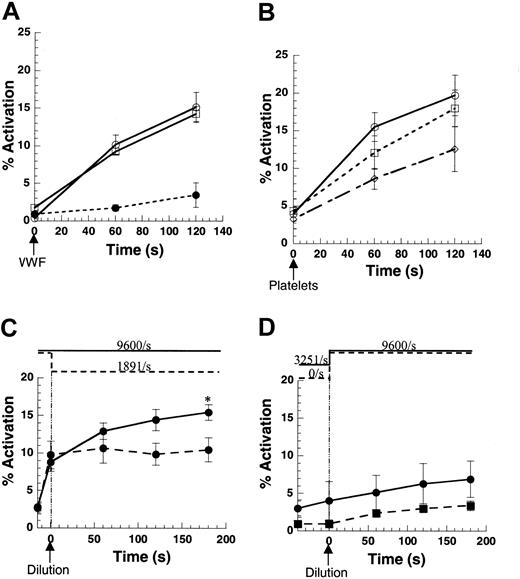
Mechanism of SIPAct.
(A) Platelets from PPACK anticoagulated blood were diluted in HEPES containing 1.5 mM Ca2+ and 100 μM PPACK to achieve concentrations of 10 × 106cells/mL. This suspension was either incubated at 37°C under static conditions (○) or was presheared at 9600/s for 1 minute (■). In both cases, at t = 0, 15 μg/mL purified VWF was added and shear at 9600/s was applied. In control runs (●), diluted PRP with platelets at 10 × 106cells/mL was sheared in the viscometer at 9600/s in the absence of exogenous VWF for the duration of the experiment. (B) Citrated PPP was placed on the 37°C plate of the viscometer under static conditions (○) or was presheared in the viscometer at either 9600/s (⋄) or 6000/s (■) for 2 minutes. At t = 0, PRP was added such that the final platelet concentration was 10 × 106cells/mL, and all samples were sheared at 9600/s. (C) Citrated PRP at 300 × 106platelets/mL was placed in a cone-plate viscometer at t = −15 seconds, and shear was applied at 9600/s for 15 seconds. At t = 0, the suspension was diluted 30-fold in HEPES containing 10 μg/mL anti-GpIb monoclonal antibody (mAb) AN-51. Following dilution, shear was maintained at 9600/s for 3 minutes (solid line) or was reduced to 1891/s (dashed lines). (D) PRP at 300 × 106platelets/mL was sheared in the viscometer at 3251/s for 45 seconds (solid line) or was maintained under static conditions (dashed line) starting at t = −45 seconds. At t = 0, the suspension was diluted 30-fold as described in panel C, and the shear rate was increased to 9600/s. *Both the increase in platelet activation following dilution, and the absolute level of platelet activation were significantly higher than all other treatments in panels C and D. Data are mean ± SEM for n = 3-5.
Mechanism of SIPAct.
(A) Platelets from PPACK anticoagulated blood were diluted in HEPES containing 1.5 mM Ca2+ and 100 μM PPACK to achieve concentrations of 10 × 106cells/mL. This suspension was either incubated at 37°C under static conditions (○) or was presheared at 9600/s for 1 minute (■). In both cases, at t = 0, 15 μg/mL purified VWF was added and shear at 9600/s was applied. In control runs (●), diluted PRP with platelets at 10 × 106cells/mL was sheared in the viscometer at 9600/s in the absence of exogenous VWF for the duration of the experiment. (B) Citrated PPP was placed on the 37°C plate of the viscometer under static conditions (○) or was presheared in the viscometer at either 9600/s (⋄) or 6000/s (■) for 2 minutes. At t = 0, PRP was added such that the final platelet concentration was 10 × 106cells/mL, and all samples were sheared at 9600/s. (C) Citrated PRP at 300 × 106platelets/mL was placed in a cone-plate viscometer at t = −15 seconds, and shear was applied at 9600/s for 15 seconds. At t = 0, the suspension was diluted 30-fold in HEPES containing 10 μg/mL anti-GpIb monoclonal antibody (mAb) AN-51. Following dilution, shear was maintained at 9600/s for 3 minutes (solid line) or was reduced to 1891/s (dashed lines). (D) PRP at 300 × 106platelets/mL was sheared in the viscometer at 3251/s for 45 seconds (solid line) or was maintained under static conditions (dashed line) starting at t = −45 seconds. At t = 0, the suspension was diluted 30-fold as described in panel C, and the shear rate was increased to 9600/s. *Both the increase in platelet activation following dilution, and the absolute level of platelet activation were significantly higher than all other treatments in panels C and D. Data are mean ± SEM for n = 3-5.
Annexin V is a sensitive marker of shear-induced platelet activation
We compared Annexin V binding, microparticle formation, and cell aggregation to determine a parameter that would sensitively report on SIPAct. PRP obtained from citrated blood was sheared at 9600/s in the viscometer. Annexin V–FITC binding to single platelets was measured before and after shear using flow cytometry, and the fraction of activated platelets was quantified (Figure 1A). Here, up to 46% of platelets displayed higher than baseline Annexin V binding after 5 minutes of shear. Depending on the cell concentration and sample volume, up to 75% of sheared platelets could be induced to bind Annexin V (data not shown). Thus, we did not observe a significant subpopulation of platelets that was unresponsive to shear-induced up-regulation of procoagulant activity. Results in experiments performed with PPACK as an anticoagulant were within 20% of the runs with sodium citrate.
Within 10 seconds of shear, a statistically significant increase in platelet activation was detected using Annexin V (Figure 1B). Incubation of platelets with blocking antibodies against GpIb, but not GpIIb-IIIa, reduced Annexin V binding. In contrast to Annexin V measurements, assays based on microparticle formation (Figure 1C) and shear-induced aggregation (data not shown) were not as sensitive in reporting on the platelet activation state. Statistically significant microparticle formation was observed only beyond 40 seconds of shear application. Overall, our results suggest that Annexin V binding is a reliable and quantitative indicator of SIPAct.
Cell-cell collisions are not necessary for SIPAct
Previous studies have reported that SIPA and VWF binding are observed only at cell concentrations greater than 50 × 106/mL.2,35 Although it is clear that cell-cell collisions are necessary for platelet aggregation, we examined whether collisions are also necessary for single platelet activation (Figure 2). PRP was supplemented with PPP to obtain platelet concentrations in the range of 10 × 106 to 300 × 106/mL, and suspensions were sheared at 9600/s. Varying cell concentrations in this range did not alter media viscosity. As seen, decreasing the cell concentration by 30-fold from 300 × 106 to 10 × 106 led to a 50% decrease in cell activation. According to the 2-body collision theory,29 36 the collision frequency at a given shear rate is proportional to the square of the cell concentration—that is, a 30-fold decrease in concentration would result in a 900-fold decrease in collision frequency. The weak dependence of platelet activation on cell concentration suggested that collisions between cells are not critical for SIPAct.
Fluid shear stress rather than shear rate controls platelet activation
We distinguished between the roles of fluid shear rate and shear stress in inducing platelet activation (Figure3). Although shear rate determines the rate and duration of encounter between cells and molecules in suspension, shear stress determines the magnitude of force applied. In the first set of experiments, platelets at 10 × 106/mL or whole blood were subjected to a range of shear rates from 0 to 9600/s (Figure 3A). In isolated platelet suspensions, we observed minimal platelet activation below 6800/s. Above this threshold shear rate, activation increased markedly with shear. Whole blood also displayed 2-phase behavior, with activation increasing sharply beyond 2200/s. Addition of 2 U/mL apyrase did not affect activation levels in whole blood runs, suggesting that Annexin V up-regulation in whole blood was independent of adenosine diphosphate (ADP) (data not shown). The threshold shear stress value of 75 dyn/cm2 (PRP fluid viscosity = 1.1 cP) for isolated platelet runs compared favorably with the corresponding value of 83 dyn/cm2 (blood viscosity = 3.8 cP) for whole blood.
In other experiments performed with isolated platelets (Figure 3B), we doubled the media viscosity in some runs by adding 1.5% wt/vol dextran or we added equal amounts of HEPES buffer in control runs. The viscosity in control runs was 1.1 cP, and the addition of dextran doubled viscosity to 2.2 cP. For a Newtonian fluid such as our dilute cell suspension, the addition of 1.5% dextran doubles the shear stress without changing the shear rate. At 9600/s, this led to a 3.3-fold increase in platelet activation (Figure 3B). In control experiments, we observed that the incubation of platelets with dextran alone for 3 minutes did not by itself induce platelet activation. Similarly, the addition of function blocking antibody against GpIb abrogated platelet activation in the presence and in the absence of dextran. Qualitatively similar results were obtained for platelets isolated from sodium citrate and PPACK anticoagulated blood. In summary, shear stress and not shear rate appeared to be the critical parameter controlling SIPAct. A threshold shear stress of 75 dyn/cm2 to 83 dyn/cm2 was necessary for platelet activation in isolated platelets and in whole blood.
Time-varying shear stresses do not promote platelet activation
In regions of arterial stenosis, platelets are subjected to time-varying shear when they enter the stenosis from a lower shear regime. The finding that SIPA is enhanced in patients with arterial stenosis has raised the possibility that, besides high shear stress, time-varying shear may also contribute to platelet activation.37 We examined this possibility in our viscometer studies. Experiments were based on our recent finding that shear rate varies with position due to secondary flow in the cone-plate viscometer under conditions applied in SIPA studies.27These positional variations in shear were more prominent at the higher cone rotation rates and for experiments with larger cone angles and sample volumes.
Experiments were performed at a constant cone rotation rate in a 0.5° cone-plate viscometer at 2 different sample volumes—either 55 or 300 μL (Figure 4). The angular velocity of the cone in both cases equaled 83.8 radians/s, which corresponded to the application of G = 9600/s under primary flow conditions. Our computations indicated that for both sample volumes of 55 μL and 300 μL, the average shear rate applied was approximately equal to the primary flow value of 9600/s (Figure4A). However, the distribution of shear rate was broader for the larger sample volume. Circulating particles in experiments with larger sample volumes were, therefore, exposed to increased time-varying stresses.
We quantified the exact magnitude of time-varying stress for the 2 volumes (Figure 4B). If the assumption of primary flow in a cone-plate viscometer is made, particles are not subjected to time-varying stresses because the shear rate is independent of position in the device. However, in real experiments, time-varying stresses are applied. Changing the volume from 55 μL to 300 μL resulted in an approximately 19-fold increase in time-varying stress.
We experimentally measured the effect of varying sample volume on SIPAct using citrated PRP (Figure 4C). Increasing the magnitude of time-varying stress by increasing sample volume did not augment platelet activation. In fact, a moderate and significant decrease in activation was observed at the higher sample volume. Similar results were obtained with PPACK anticoagulated blood. We speculate that this decrease could be attributed to a reduction in the exposure time of platelets and VWF to regions with large shear stresses. For instance, at any given time, though the volume fraction of particles experiencing a local shear rate greater than 9500/s was 98.8% in the 55 μL volume run, it was only 47% for the 300 μL volume run (Figure 4A). Overall, under the conditions tested, time-varying stresses did not enhance SIPAct.
Two-step mechanism for SIPAct
Arguments in the literature support the propositions that fluid shear primarily influences VWF function and that it primes blood platelets.1 4 We attempted to use our sensitive Annexin V assay to further clarify the mechanism of SIPAct.
In some runs (Figure 5A), we presheared platelets before the addition of 15 μg/mL purified VWF isolated from human plasma cryoprecipitate. VWF concentration used here is comparable to that in healthy donor blood. In these runs, PRP obtained from PPACK anticoagulated blood was diluted 35- to 40-fold in HEPES buffer to obtain a final platelet concentration of 10 × 106cells/mL. Subjecting these cells alone to shear at 9600/s did not result in significant platelet activation, confirming that the residual VWF concentration was low in this system (Figure 5A). The addition of purified VWF to platelets in the absence of shear or on the application of low shear (below 6000/s) did not result in significant activation (data not shown). The addition of VWF to 1-minute presheared platelets and to unsheared controls resulted in similar activation levels when shear was applied at 9600/s (Figure 5A). These results indicate that fluid-flow–mediated changes on platelets, if any, are rapidly reversible.
In other runs (Figure 5B), we presheared PPP from citrated blood before the addition of platelets. Here, preshearing PPP for 2 minutes at either 6000/s or 9600/s reduced subsequent platelet activation in the presence of shear at 9600/s. This loss in VWF activity was shear dependent. In Western blots, we did not detect the loss of plasma VWF to the viscometer surface (data not shown). A possible explanation for the reduced VWF activity is the shear-dependent proteolytic cleavage of VWF multimers.38 Together, the results of Figure 5A-B indicate that VWF, platelet GpIb, and fluid shear must be present simultaneously for SIPAct to occur.
To further resolve the sequence of events leading to SIPAct, we addressed the hypothesis that platelet GpIb must first bind VWF under shear and that subsequently fluid forces applied on these VWF-bound cells induces activation. Experiments were performed in which VWF was present in solution in the first phase of each run, and its interaction with platelet GpIb was prevented in the second phase. Here, PRP with 300 × 106 platelets/mL was subjected to shear at 9600/s for 15 seconds in the first phase, before dilution in 30-fold excess HEPES buffer containing 10 μg/mL anti-GpIb antibody (Figure5C). Thus, VWF-GpIb binding was prevented after dilution. Simultaneously, at the time of dilution, the shear rate was kept at the same level or was reduced to 1891/s for the second phase. Although platelet activation increased significantly by 6.5% when the shear rate was maintained at 9600/s in the second phase, there was a negligible increase in activation when the shear rate was decreased to 1891/s. These results suggest that high shear forces, even in the absence of VWF in suspension, can induce platelet activation in the second phase.
Additional runs were performed to examine the requirement for shear in the first phase (Figure 5D). Here, we observed that platelet activation was low when cells maintained under static conditions in the first phase were diluted and sheared in the second phase. This indicates that shear, in addition to VWF, is required in the first phase for subsequent SIPAct. In another run, platelets were sheared at 3251/s for 45 seconds in the presence of VWF before dilution and shear application at 9600/s. This time only a 2.9% increase in platelet activation was observed (Figure 5D). The number of platelet-VWF collisions was identical in samples sheared at 9600/s for 15 seconds (Figure 5C) and those sheared at 3251/s for 45 seconds (Figure 5D) because collision frequency is a linear function of shear rate.36 The statistically higher level of platelet activation observed in the former case suggests that fluid forces, rather than number of platelet-VWF encounters, contribute to functional changes in the first phase. Overall, the results support a 2-step mechanism of platelet activation. Fluid shear and VWF are required for the first step in which VWF-GpIb binding likely occurs. Subsequently, platelet activation requires fluid forces but not free VWF in suspension.
SLS analysis of unsheared VWF
Recently, a few studies have used atomic force microscopy to examine the morphology of immobilized VWF on the application of shear.39 40 Motivated by these studies, we undertook light scattering experiments to quantify shear-induced changes in VWF morphology in suspension. For these runs, 5 different batches of VWF were purified from human blood cryoprecipitate. Some batches consisted of blood from an individual donor, while others were prepared by pooling cryoprecipitate from 2 to 3 donors. Although there was some variability in VWF size with preparation, the response to shear was qualitatively identical. Representative results are presented, and variability among samples is discussed.
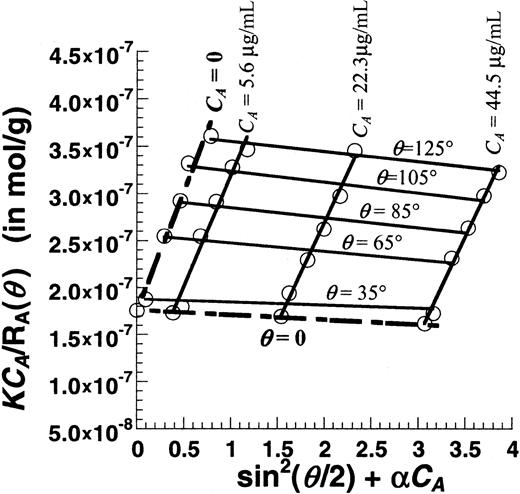
Figure 6 is a Zimm plot for human VWF under native unsheared conditions using SLS. For these runs, purified VWF samples at concentrations (CA) from 0.0045 to 0.045 mg/mL were used, and light-scattering detection angles (θ) varied from 35° to 145°. Fitting the experimental data yielded a molecular weight (MWt) of 5.7 × 106 Da, a radius of gyration (Rg) of 63.6 nm, and a second virial coefficient (A2) of −1.53 × 10−4mL × mol/g2. Depending on the preparation, the molecular weight of VWF typically varied from 5 × 106 to 15 × 106 Da, andRg varied from 60 to 150 nm.A2 was small in all cases indicating that, under our experimental conditions, it was possible to determine molecular weight and size by performing SLS analysis at any single protein concentration (see online supplemental document). This approach was therefore used in subsequent studies that examined the effect of shear stress.
Zimm plot for purified human VWF.
Unsheared VWF samples at 3 different concentrations (CA = 5.6, 22.3, and 44.5 μg/mL) were analyzed using SLS. Detector angles (θ) were varied from 35° to 145° with respect to the incident beam. Discrete points depict experimental data. Solid lines are used to fit the data at either constant VWF concentration (CA) or constant detector angles (θ). Data extrapolated toCA = 0 and θ = 0 are depicted by broken lines. The Zimm plot shown here can be used to determine the MWt, Rg, and A2. Hereα is an arbitrary constant that equals 69 000. MWt was estimated to equal 5.7 × 106 Da,Rg was 63.6 nm, and A2was −1.53 × 10−4 mL × mol/g2.
Zimm plot for purified human VWF.
Unsheared VWF samples at 3 different concentrations (CA = 5.6, 22.3, and 44.5 μg/mL) were analyzed using SLS. Detector angles (θ) were varied from 35° to 145° with respect to the incident beam. Discrete points depict experimental data. Solid lines are used to fit the data at either constant VWF concentration (CA) or constant detector angles (θ). Data extrapolated toCA = 0 and θ = 0 are depicted by broken lines. The Zimm plot shown here can be used to determine the MWt, Rg, and A2. Hereα is an arbitrary constant that equals 69 000. MWt was estimated to equal 5.7 × 106 Da,Rg was 63.6 nm, and A2was −1.53 × 10−4 mL × mol/g2.
Fluid shear induces VWF self-association in suspension
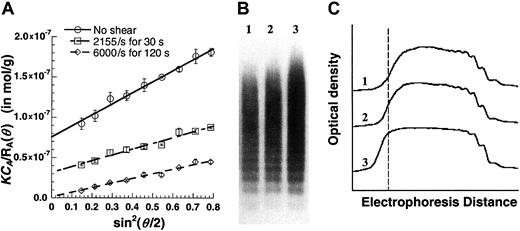
We assessed the effect of fluid shear on the morphology and size of VWF (Figure 7). Purified VWF at a concentration of approximately 0.1 mg/mL was sheared in a cone-plate viscometer, and SLS analysis was performed on the sheared samples (Figure 7A). MWt and Rg values were estimated. The unsheared purified VWF used for Figure 7A had a molecular weight of 13.3 × 106 Da and a radius of gyration of 71.7 nm. Subjecting this VWF to shear at 2155/s for 30 seconds resulted in an increase in MWt to 32.0 × 106 Da andRg to 82.0 nm. Shearing samples at 6000/s for 2 minutes further increased MWt to 847.5 × 106 Da andRg to 341.3 nm. An increase in VWF molecular weight in response to shear was observed in all our preparations, though it was diminished (only doubled) in one preparation. In addition, the increase in molecular weight was augmented at higher shear rates and longer shearing times. Table1 presents a summary of light-scattering results. As seen, DLS analysis of the samples compared well with the SLS data. Although VWF aggregates remained stable up to 5 hours after shear, the addition of 0.1% SDS caused rapid, albeit incomplete, dissociation of sheared samples (data not shown). Taken together, the results suggest that VWF noncovalently self-associates under hydrodynamic shear.
Effect of fluid shear on VWF size.
Purified VWF (125 μL) at approximately 0.1 mg/mL was maintained under static conditions or was sheared in a viscometer at specified shear rates for fixed times. (A) Samples were diluted 8-fold in HEPES buffer and immediately subjected to SLS. MWt and Rgwere determined from this plot. MWt equals 1/(y-axis intercept). An increase in VWF homotypic aggregate size and MWt was observed with shear and time. Data are mean ± SEM for 2 shear runs with a single batch of VWF. (B) Western blot analyses of unsheared and sheared samples demonstrate qualitative increases in VWF size. Lane 1 indicates unsheared VWF; lane 2, VWF sheared at 2155/s for 30 seconds; lane 3, VWF sheared at 6000/s for 120 seconds. An equal amount of protein was loaded in each lane. (C) Densitometry tracing of the Western blot in panel B. Dashed line corresponds to highest MWt of the unsheared sample. Application of shear causes larger aggregates to appear to the left of this line. Results are representative of 3 independent experiments.
Effect of fluid shear on VWF size.
Purified VWF (125 μL) at approximately 0.1 mg/mL was maintained under static conditions or was sheared in a viscometer at specified shear rates for fixed times. (A) Samples were diluted 8-fold in HEPES buffer and immediately subjected to SLS. MWt and Rgwere determined from this plot. MWt equals 1/(y-axis intercept). An increase in VWF homotypic aggregate size and MWt was observed with shear and time. Data are mean ± SEM for 2 shear runs with a single batch of VWF. (B) Western blot analyses of unsheared and sheared samples demonstrate qualitative increases in VWF size. Lane 1 indicates unsheared VWF; lane 2, VWF sheared at 2155/s for 30 seconds; lane 3, VWF sheared at 6000/s for 120 seconds. An equal amount of protein was loaded in each lane. (C) Densitometry tracing of the Western blot in panel B. Dashed line corresponds to highest MWt of the unsheared sample. Application of shear causes larger aggregates to appear to the left of this line. Results are representative of 3 independent experiments.
Molecular weights and sizes of sheared VWF
| Shear applied . | Molecular weight, Da . | Radius of gyration, nm . | Hydrodynamic radius, nm . |
|---|---|---|---|
| No shear | 9.6 × 106 (± 3.7 × 106) | 97.1 (± 29.6) | 68.2 (± 19.2) |
| 2155/s for 30 s | 25.1 × 106 (± 6.9 × 106) | 113.8 (± 27.0) | 91.3 (± 22.9) |
| 6000/s for 120 s | 695.5 × 106 (± 152 × 106)* | 394.8 (± 117.7) | 466.4 (± 95.6)* |
| Shear applied . | Molecular weight, Da . | Radius of gyration, nm . | Hydrodynamic radius, nm . |
|---|---|---|---|
| No shear | 9.6 × 106 (± 3.7 × 106) | 97.1 (± 29.6) | 68.2 (± 19.2) |
| 2155/s for 30 s | 25.1 × 106 (± 6.9 × 106) | 113.8 (± 27.0) | 91.3 (± 22.9) |
| 6000/s for 120 s | 695.5 × 106 (± 152 × 106)* | 394.8 (± 117.7) | 466.4 (± 95.6)* |
Results are presented as mean (± SEM) for n = 3 VWF isolations.
Molecular weights and radii of gyration were obtained from SLS analysis and DLS analysis, respectively.
Significantly different from the unsheared sample.
Western blotting of sheared and unsheared VWF was performed to confirm the presence of VWF aggregates following shear (Figure 7B). For this analysis, each lane of the gel was loaded with equal amounts of protein under nonreducing conditions. Blots (Figure 7B) and densitometry analysis (Figure 7C) confirm the occurrence of larger VWF moieties in sheared samples. These are presumably VWF aggregates that were resistant to 0.1% sodium dodecyl sulfate (SDS) treatment.
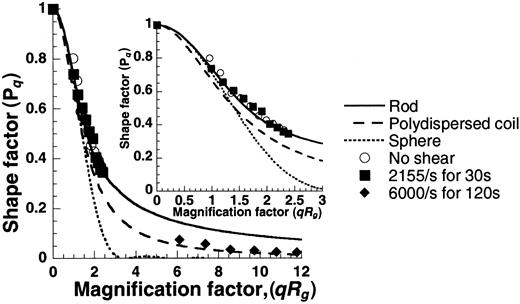
Sheared VWF molecules resemble polydispersed coils
Plots of shape factor versus magnification factor (Figure8) generated using the SLS data were compared with theoretical predictions for spheres, rods, and polydispersed coils. Results indicate that the unsheared samples appeared rodlike, and the sheared samples resembled polydispersed coils. We observed VWF self-association in our experiments, but macroscopic morphologic extension of individual molecules on the application of shear, if any, were not discernible.
Shape of unsheared and sheared VWF.
SLS data from Figure 7A were used to determine the shape of VWF by plotting the shape factor (Pq) against the magnification factor (qRg). Experimental points under the various conditions are depicted as discrete points, and theoretical predictions of PqversusqRg for spheres, rods, and polydispersed coils are presented as smooth lines (see online supplemental document for details). The unsheared sample appears rodlike, and the sheared sample resembles a polydispersed coil. The inset offers a closer look atqRg values from 0 to 3.
Shape of unsheared and sheared VWF.
SLS data from Figure 7A were used to determine the shape of VWF by plotting the shape factor (Pq) against the magnification factor (qRg). Experimental points under the various conditions are depicted as discrete points, and theoretical predictions of PqversusqRg for spheres, rods, and polydispersed coils are presented as smooth lines (see online supplemental document for details). The unsheared sample appears rodlike, and the sheared sample resembles a polydispersed coil. The inset offers a closer look atqRg values from 0 to 3.
Discussion
Aspects of fluid flow controlling platelet activation
We examined the role of various aspects of fluid flow in mediating SIPAct. In experiments with varying cell concentrations, we observed that though high cell concentrations may enhance platelet activation, the activation levels did not correlate with cell collision frequency. Further, experiments with varying media viscosity demonstrated that platelet activation is controlled by fluid shear stress rather than by shear rate. Thus, it is the magnitude of hydrodynamic force applied and not the number of cell/molecular collisions that controls SIPAct. The minimum shear stress requirement was approximately 80 dyn/cm2 for platelet activation in isolated platelets and whole blood.
In studies designed to contrast the effects of constant high shear versus time-varying shear, we observed similar levels of platelet activation. We note that even under constant linear shear, cell surface receptors and soluble molecules, by virtue of their rotational motion, experience rapid force variations.26 The frequency of force loading in this case depends on the time-period of cell/molecular rotation. In addition to this, molecules in our time-varying shear experiments are subjected to a second, slower force-loading mechanism because of their translational motion through regions of varying shear. Our results suggest that platelets and VWF respond primarily to the rapid force variations from constant high shear rather than from the slower force-loading mechanism.
Two-step mechanism of shear-induced platelet activation
We examined the contributions of GpIb, VWF, and fluid shear in inducing SIPAct. Our experiments reveal 2 distinct phases for this process. Fluid shear and VWF are required in the first phase in which VWF-GpIb binding likely occurs. The proposition that shear forces enhance VWF-GpIb binding is supported by direct binding studies.35 This binding may not result in cell activation. Subsequently, in the second phase, platelet activation requires fluid forces only. Thus, VWF-GpIb binding is separable from platelet mechanotransduction.
The exact target of fluid forces in the second phase remains unresolved. It is possible that forces applied on the VWF-GpIb complex may be responsible for mechanotransduction. In support of this, a recent study shows that though platelets interact with VWF-bearing substrates over a range of shear, the interacting cells exhibit enhanced calcium fluxes at the higher shears.9 We note that the recombinant VWF A1 domain added to our suspension assay at concentrations up to 150 μg/mL did not itself induce platelet activation at 9600/s (data not shown), even though this molecule binds platelet GpIb under static conditions.24 In the context of the above model, it appears that the lower force applied on the smaller A1 domain–GpIb complex may be insufficient to induce activation. Others31 have shown that larger VWF multimers that would presumably lead to larger forces once bound to GpIb are more effective in mediating platelet aggregation.
In light of the 2-step model of SIPAct, we estimated the magnitude of hydrodynamic force applied on VWF and GpIb (online supplemental document). At 9600/s, we estimated that globular portions of soluble VWF and GpIb experienced forces on the order of 0.1 pN. When complexed with VWF, GpIb experienced significantly higher forces of approximately 1.5 pN at the same shear rate. This supports the proposition that fluid forces acting on the GpIb-VWF complex may trigger mechanotransduction. In comparison, in the flow chamber model of vascular injury,41 the drag force applied on platelets interacting with substrate is 35 pN at 1000/s.42 This difference in force requirement for SIPAct in suspension and on substrates could be caused by several factors. Platelets rolling on VWF substrates could be more readily activated than cells in suspension, which require approximately 10 seconds (Figure 1B). Alternatively, multiple VWF-GpIb bonds may be engaged in the flow chamber experiments, and the applied force may be distributed among several bonds.
VWF morphology and self-association in suspension
We applied light scattering to examine whether the morphology of soluble VWF is altered on the application of fluid shear. In these studies, we took advantage of the fact that light scattering allowed rapid analysis of proteins in the absence of sample fixation or destruction. We noted that light scattering was skewed to report on larger molecules because the intensity of scatter was proportional to the third power of molecular size. Thus, these experiments report the weight-averaged molecular weight, which is much larger than the number-averaged value.
Our VWF preparations consisted of up to 10 to 30 500 kDa protomeric units, with molecular weights on the order of 5 × 106 to 15 × 106 Da. On the application of shear, we observed increases in the molecular weight and size of VWF at shear rates down to 2155/s. Western blot analysis confirmed the increase in molecular weight. The shear-induced VWF aggregates were partially dissociated by 0.1% SDS treatment, thereby suggesting the noncovalent nature of the self-association.
Several lines of evidence indicate that fluid forces rather than increased numbers of VWF-VWF collisions were responsible for shear-induced VWF aggregation. Although aggregation occurred in sheared samples, samples stored in the absence of shear for 3 days did not exhibit significant aggregation (data not shown). In this regard, samples stored in situ for 3 days experienced approximately 3 orders of magnitude more intermolecular collisions than samples sheared at 6000/s for 2 minutes. Further, though the number of intermolecular collisions is a linear function of shear,36 the extent of aggregation increased nonlinearly with applied shear.
While this work was in progress, Savage et al23 published a report on the association of soluble VWF from suspension to collagen-immobilized VWF. The authors speculate that this self-association may provide an additional mechanism controlling thrombosis at sites of vascular injury. Our current studies now demonstrate that VWF self-association can be shear mediated. The mechanism of VWF self-association and its contribution to SIPAct remains unresolved. Loscalzo et al43 have previously demonstrated that VWF protomers spontaneously self-associate and that this has a function-enhancing effect. Future studies may determine whether analogous mechanisms are responsible for protomer association and shear-induced self-association of multimeric VWF.
We thank Kok Keong Chain and Ken-Tye Yong for help with the light-scattering experiments and Dr Johannes Nitsche for discussions regarding the nature of force applied on biomolecules.
Prepublished online as Blood First Edition Paper, November 27, 2002; DOI 10.1182/blood-2002-05-1550.
The online version of the article contains a data supplement.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 U.S.C. section 1734.
References
Author notes
Sriram Neelamegham, Bioengineering Laboratory, Department of Chemical Engineering, 906 Furnas Hall, State University of New York, Buffalo, NY 14260; e-mail:neel@eng.buffalo.edu.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal