Abstract
Randomized clinical trials remain the gold standard to establish efficacy and safety of new treatments. In acute myeloid leukemia, large trials have been associated with gradual improvement in outcome over 2 decades in younger patients without major differences emerging between treatments. By contrast, in older patients, improvement has been minimal, which justifies a new approach to identifying effective treatments. Given the urgent unmet need, and with the emergence of several novel agents or combinations that are likely to be expensive, large benefits are probably required to change clinical practice. To address this issue, we have evolved a “Pick a Winner” randomized progressive design with a rolling incorporation of novel treatments (drug X), which has been tested in older patients with acute myeloid leukemia. The rationale, operational characteristics, and initial experience of such an approach in the context of the United Kingdom National Cancer Research Institute AML16 trial are presented.
Introduction
Randomized clinical trials in acute myeloid leukemia (AML) remain the cornerstone of evidence-based practice, but the demographics, relative rarity, and biologic heterogeneity of the disease present a challenge to trialists. The majority of patients with AML are older than 65 years, and this group has traditionally been substantially under-represented in clinical trials.1,2 This is further compounded by the substantial heterogeneity of the disease at the cytogenetic and molecular level, with striking implications for prognosis irrespective of treatment used. Many trials have been undertaken without any statistical, let alone clinically important, differences being shown between interventions.3,4 Such studies have involved large numbers of patients to meet traditional statistical requirements. For example, the Medical Research Council/National Cancer Research Institute (NCRI) AML group in the United Kingdom addressed 16 randomized questions with a total of 14 000 randomizations in patients younger than 60 years between 1998 and 2009 without showing any overall difference in any treatments. In younger patients, however, there was an improvement in survival for most subgroups during this time period, supporting the contention that supportive care improvements have made an important contribution. A portfolio of trials based on an intensive chemotherapy approach for older patients evaluated 12 interventions with 7500 randomizations with no significant differences observed, but in this population little, if any, improvement has been seen.4
Although a negative result from a trial has its value, consideration must be given to strategy if at the same time no overall improvement is being seen.5,6 In our experience in younger patients, the average number of randomizations per intervention was approximately 900, driven by conventional statistical power requirements. However, it could be argued that an interim futility analysis could have allowed more questions to be asked and treatments not associated with improvement to be stopped earlier. For example, after half the requisite number of events had accrued, most comparisons did not show any difference, meaning that there would have to have been a substantial (and unlikely) benefit in the second half of the trial to provide the hoped-for effect size. However, with overall survival as an end point, sufficient follow-up is required to see enough events, and it is probable that, by the time half the requisite number of events had been observed, recruitment would be virtually complete. Although the randomization could have been closed and another question asked while events accrued, subsequent trials are usually conditioned by the outcome of the current trial, so this would have been problematic.
In older patients, similar concerns arise but are exacerbated by the overall lack of improvement. The challenge here is both to improve response and in particular to improve the duration of response, the latter of which again requires sufficiently long follow-up to see the requisite number of events.
There is, however, a third patient group: older patients who are not offered, or do not wish to receive, a conventional intensive chemotherapy approach. There has historically been no standard of care beyond palliative oral chemotherapy to control the white blood count, and optimum supportive care. These patients represent a group where new treatments are urgently needed and could be developed more rapidly with a new strategic approach. Effective new therapies identified in this context may well become applicable in the other age groups, whereas ineffective treatments could be eliminated. Because outcomes are so poor (with a median survival typically of 2-3 months), the need is for clinically important benefits, rather than minor incremental improvements. Taking as a starting point the work by Parmar et al5 and Royston et al,7 particularly in Ovarian Cancer, we have developed and adopted such an approach in this patient population, which we designate “Pick a Winner.”
Pick a Winner design
The Pick a Winner design used in AML is essentially a modification of the “Multi Arm Multi Stage” (MAMS) design of Royston et al.7 In the MAMS design, there are (at least) 2 stages: in the first, patients are randomized between a number of different novel treatments and a control standard of care. To proceed to the second stage, a novel treatment must show at least a prespecified degree of benefit at the end of the first stage on a relevant intermediate or surrogate outcome measure compared with the control arm. The first part of the trial acts as a sifting mechanism to allow unpromising treatments to be dropped without the potential waste of proceeding to a full phase 3 trial. In other words, it is designed to identify promising treatments by eliminating those with little likelihood of benefit: the residuum will then be enriched for valuable treatments. This approach is incorporated in the Pick a Winner design, but here there is an explicit emphasis on a rolling process of drug discovery. At any one time, patients can be randomized between a number of novel treatments and control. However, not all of the treatments are necessarily at the same stage of evaluation. New drugs (“drug X”) can be added at any time; some drugs may pass the various hurdles, and others may be dropped. The original 2-stage MAMS design7 with a single elimination hurdle is refined by performing 2 preliminary evaluations, to increase the chances of identifying treatments that are unlikely to provide the necessary clinical benefit. In addition, whereas in the MAMS design7 the continuation criteria were based on the critical value of a statistical test, in this instance a Pick a Winner design looks for a prespecified improvement in outcomes irrespective of significance. Finally, in the context of the clinical need, the process is intended to be rapid: it is important to sift treatments rapidly, both by evaluating after a relatively small number of patients and also using end points that are reached early and where the minimal clinically relevant difference is relatively large. Both of these conditions can be met in AML in the older patient unsuitable for intensive treatment. In this way, drug discovery is speeded up by reducing the amount of time spent on investigation of treatments that do not improve outcome, and identifying those with promise.
Patients entering the trial are randomized between standard of care and a number of experimental treatment arms. Some patients may not be eligible for certain arms of the trial, for example, on renal function criteria; they will only be randomized between those arms for which they are eligible. All novel treatments are only compared against standard of care and not each other, with the comparison only between patients who were randomized between the novel therapy and standard of care. So, a patient not eligible for a particular novel therapy for whatever reason will not contribute to any evaluation of that treatment. This approach maintains a strict randomized comparison to help eliminate selection biases. At 2 predetermined points, defined either by the number of patients or events (depending on choice of end point) in each 2-way comparison, outcomes are compared in confidence by the independent Data Monitoring Committee. If the treatment does not look likely to achieve the prespecified improvement, it is recommended to be discarded. Importantly, to allow for flexibility, new treatments (drug X) may be added to the protocol at any time, by protocol amendment. Only those treatments that pass the interim analyses continue to a full phase 3 trial now with overall survival as primary end point.
There is clearly a balance to be drawn as to when the arms are examined for promise. Too early, and results may not be informative; too late, and there is likely to be little saving in patients compared with a classic trial design. Within these constraints, there is a certain amount of flexibility in the precise choice of analysis points. The Pick a Winner approach adopts 2 testing points, and as the aim is for rapid rejection of unpromising treatments, both tests occur by the halfway point of the trial in terms either of patients or events (depending on the outcome measure): the first, after one-fourth the number of patients (or the number of events), should help eliminate treatments that are worse than standard of care; the second, at one-half the number of patients or events, should help restrict attention only to those treatments that look sufficiently promising and are likely to achieve the aspiration for improvement, for example, doubling the remission rate.
As with the timing of the examination points, there is a balance to be struck in terms of the continuation requirements at each test. If criteria are too strict, then worthless treatments will be eliminated as intended, but there is also a real risk of eliminating worthwhile treatments; if too lax, too many worthless treatments will be carried forward, which effectively returns to the situation where there is no stopping rule for futility. The precise details of the stopping rule will clearly depend on the characteristics of the treatment being examined and may indeed vary from treatment to treatment, but will be based on the size of benefit that is considered worthwhile, and the extent to which power to identify worthwhile treatments, and economy in rejecting futile treatments is important.
One important feature of the Pick a Winner (and indeed the MAMS approach) is the need for contemporaneous randomization, and proper randomized comparison, against the control arm. In this way, the design differs substantially from the so-called Pick the Winner approach of Sargent et al,8 which aims to identify a candidate for a future phase 3 trial. By contrast, here phase 3 evaluation is included as an intrinsic part of the design. Consequently, strict randomization against a control arm is mandatory. Different drugs may have slightly different eligibility requirements; therefore, different arms may recruit slightly different types of patients, with different predicted outcomes. The comparison within randomization only ensures that any differences seen are not the result of different types of patients in the different arms. The salient features of the Pick a Winner design are listed in Table 1.
Essential aspects of a Pick a Winner design
| Randomization between a control arm and a number of novel treatments, with comparisons only between patients randomized between a given novel treatment and control |
| Ability to add new treatments (drug X) in a rolling program by protocol amendment |
| Rapid ascertainment of outcome, or a meaningful surrogate |
| Requirement that the minimal clinically relevant difference is relatively large |
| Evaluation after a small proportion (eg, one-fourth and one-half) of the required number of patients or events |
| Suitable continuation criteria |
| Randomization between a control arm and a number of novel treatments, with comparisons only between patients randomized between a given novel treatment and control |
| Ability to add new treatments (drug X) in a rolling program by protocol amendment |
| Rapid ascertainment of outcome, or a meaningful surrogate |
| Requirement that the minimal clinically relevant difference is relatively large |
| Evaluation after a small proportion (eg, one-fourth and one-half) of the required number of patients or events |
| Suitable continuation criteria |
Implementation of Pick a Winner in AML
AML in older patients who are not considered suitable for intensive therapy satisfies the criteria set out in Table 1 because outcomes are poor in this patient population9,10 and small benefits unlikely to be clinically and economically worthwhile. To establish a baseline standard of care, our Leukemia Research Fund (now Leukemia and Lymphoma Resarch) United Kingdom AML14 trial found that low dose Ara-C (LDAC) was superior to best supportive care with intermittent hydroxyurea, without any increase in toxicity or supportive care.11 The survival benefit was however restricted to the 18% of patients who achieved complete remission (CR; median overall survival, 19 months compared with 2 months in those who failed to respond). This observation endorsed the commonly accepted belief that achieving CR was a prerequisite for survival benefit. Consequently, given the type of therapeutic agents being investigated, CR was chosen as the meaningful early end point which was a suitable surrogate for survival in the Pick a Winner design in this patient group. In light of the fact that treatments are likely to be expensive, a clinically worthwhile difference in survival, such as a doubling of 2-year survival to 20%, was considered feasible. As survival to 2 years in AML14 occurred only in patients reaching CR, a doubling of the proportion alive at 2 years would require a doubling of the proportion entering CR: given the remission rate observed with LDAC, this would equate to an improvement in remission from approximately 15% to 30%.
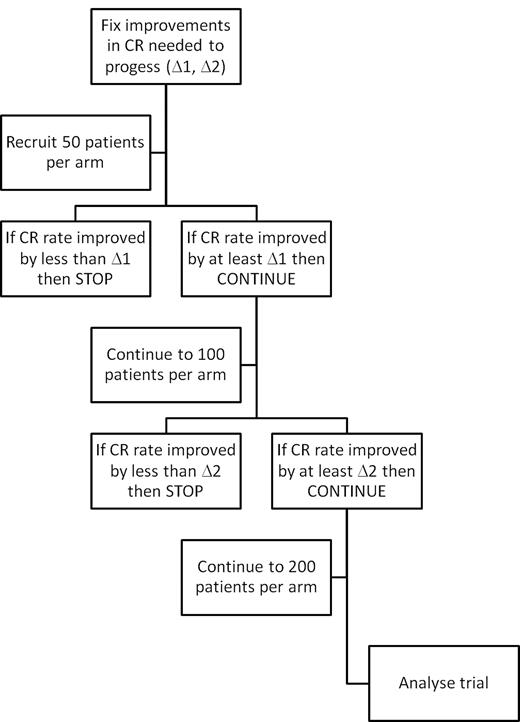
Next, the continuation thresholds at each stage need to be set. As there are potentially a number of randomized comparisons in the trial, significance is set at P < .01. Based on the assumptions in the preceding paragraph concerning the minimal clinically relevant difference, to achieve at least 80% power in a classic trial would require approximately 200 patients per arm, a number that will also provide sufficient power in the comparison of overall survival. Consequently, interim examinations for continuation are scheduled after 50 and 100 patients per arm. If the desired improvement in CR rates (measured as an absolute difference) is seen, then the trial can continue, with an ultimate overall recruitment of 200 patients per arm (Figure 1) and a primary outcome measure of overall survival.
Flow chart for a Pick a Winner design showing 2 interim analyses for efficacy.
It remains to determine the precise continuation criteria. Based on the requirement for a doubling in remission rate from 15% to 30%, a computer simulation was performed, running 150 000 virtual trials of 200 patients per arm over a variety of cut-offs. For each pair of continuation criteria (increments in CR rates after 50 and 100 patients per arm), it is therefore possible to determine with great certainty the power (the proportion of significant trials) for a worthwhile treatment, and the average size of trial for a worthless treatment (which we term the futility size). Table 2 shows these details for a variety of cut-offs: note that the minimum trial size possible under this arrangement is 50 patients per arm. As noted in the preceding section, higher power is associated with greater futility size; very nearly all the worthwhile treatments will pass the criteria but so will a great number of worthless or even adverse ones. Conversely, requiring greater economy (smaller futility size) has a concomitant effect on power. In Table 2, the footnoted cells (“†”) represent a reasonable trade-off between power and sample size: one possible requirement is for a 2.5% improvement in CR rate at 50 patients per arm, and a 7.5% improvement in CR rate after 100 patients per arm. In these circumstances, there is 79% power to detect an increase in remission rate from 15% to 30% at P < .01.
Probability of rejecting at either 50 or 100 patients, and average arm size for a worthless treatment (no benefit), and power, and average arm size for a worthwhile treatment (15% improvement in CR) based on a baseline CR rate of 15%
| Critical improvement in CR rate at 100 patients (Δ)2, % . | Critical improvement in CR rate after 50 patients (Δ1) . | ||||
|---|---|---|---|---|---|
| 0%, % (no.) . | 2.5%, % (no.) . | 5%, % (no.) . | 7.5%, % (no.) . | 10%, % (no.) . | |
| 2.5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 72 (106) | — | — | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 93 (195) | — | — | — | — |
| 5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 82 (96) | 85 (82)† | — | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 92 (194) | 89 (188)† | — | — | — |
| 7.5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 93 (85) | 93 (74)† | 94 (68)† | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 88 (188) | 85 (184)† | 83 (179)† | — | — |
| 10 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 97 (81) | 97 (70) | 97 (65) | 97 (61) | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 81 (181) | 79 (177) | 78 (173) | 75 (168) | — |
| 15 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | > 99.5 (78) | > 99.5 (67) | > 99.5 (62) | > 99.5 (59) | > 99.5 (56) |
| Probability of accepting worthwhile treatment, power (mean size per arm) | |||||
| 72 (145) | 71 (143) | 70 (140) | 68 (137) | 64 (133) | |
| Critical improvement in CR rate at 100 patients (Δ)2, % . | Critical improvement in CR rate after 50 patients (Δ1) . | ||||
|---|---|---|---|---|---|
| 0%, % (no.) . | 2.5%, % (no.) . | 5%, % (no.) . | 7.5%, % (no.) . | 10%, % (no.) . | |
| 2.5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 72 (106) | — | — | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 93 (195) | — | — | — | — |
| 5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 82 (96) | 85 (82)† | — | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 92 (194) | 89 (188)† | — | — | — |
| 7.5 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 93 (85) | 93 (74)† | 94 (68)† | — | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 88 (188) | 85 (184)† | 83 (179)† | — | — |
| 10 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | 97 (81) | 97 (70) | 97 (65) | 97 (61) | — |
| Probability of accepting worthwhile treatment, power (mean size per arm) | 81 (181) | 79 (177) | 78 (173) | 75 (168) | — |
| 15 | |||||
| Probability of rejecting treatment early if worthless* (mean size per arm) | > 99.5 (78) | > 99.5 (67) | > 99.5 (62) | > 99.5 (59) | > 99.5 (56) |
| Probability of accepting worthwhile treatment, power (mean size per arm) | |||||
| 72 (145) | 71 (143) | 70 (140) | 68 (137) | 64 (133) | |
— indicates not applicable.
A treatment is rejected early if the critical improvements are not seen.
Cut-offs giving good balance between power and futility size.
The statistical validity of the MAMS design has already been discussed,7 and Pick a Winner, as a specific case of MAMS, is therefore likewise valid: it produces an acceptable rate of false positive results. The important observation is that the trial is one with a variable number of patients. So long as the trial is reported at the point of closure, the estimate of effect size is unbiased, and P values are correct. The results of the computer-simulated studies used to derive the power and futility size demonstrate that, in the specific case of AML16, so long as comparisons are reported at the point of closure, the results are valid.
Advantages of the Pick a Winner design
Clearly, the option to close unpromising arms for futility has the ethical and practical advantage that patients are not randomized where there is little chance of them achieving a worthwhile benefit. However, a greater efficiency comes from the fact that a number of novel treatments are simultaneously compared against standard of care. If one compares the first stage of a Pick a Winner design with 3 novel treatments with 3 separate trials of individual agents, in the individual scenario, 300 patients are required (3 × (2 × 50)). For Pick a Winner, only 200 patients are required (Table 3). In the individual scenario, if a drug fails to progress, then the 50 patients allocated to control in that study cannot be used elsewhere. The cost in patient numbers of jettisoning the worthless drug is 100 patients. But in the Pick a Winner approach, those 50 control patients are used in comparisons of drug Y and drug Z, meaning that the “cost” is only those 50 patients drawing drug X. Conversely, if drug X is a winner, then the trials of drug Y and drug Z have a control arm, which is suddenly not relevant as there is no comparison with drug X. In the Pick a Winner design, either drug X can become standard of care, or a “doctor's choice” control arm could be introduced, and the first part of the trial before control arm modification can be meta-analyzed with the revised protocol.
Testing of 3 novel treatments under a standard model of sequential or parallel development and in a Pick a Winner design
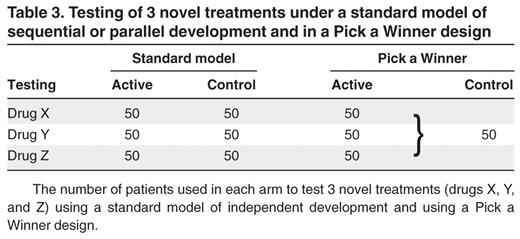
The number of patients used in each arm to test 3 novel treatments (drugs X, Y, and Z) using a standard model of independent development and using a Pick a Winner design.
In addition, given that the administrative process of setting up a new trial is one of the frustrating time limiting steps, the facility to introduce new treatments by protocol amendment is a key advantage.
Experience of Pick a Winner in the NCRI AML 16 trial
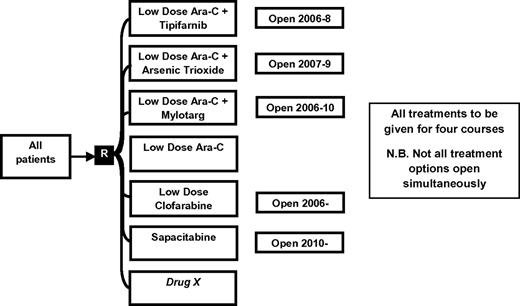
The AML16 trial (ISRCTN 11036523) initially included a randomization between LDAC and 4 novel treatment options: clofarabine, LDAC combined with the immunoconjugate gemtuzumab ozogamicin (GO), LDAC plus arsenic trioxide, and LDAC plus the farnesyl transferase inhibitor, tipifarnib (Figure 2). Continuation criteria were as set out in “Implementation of Pick a Winner in AML” to progress past 50 patients per arm, an improvement of 2.5% in remission rates was required; and those who then satisfied the requirement for a 7.5% difference in remission rates after 100 patients per arm progressed to a full 200 patient per arm study with survival as the primary outcome. At the outset of AML16, 108 patients had already been recruited to a comparison of LDAC versus LDAC plus GO as part of the AML14 trial. The Data Monitoring and Ethics Committee (DMEC) applied the initial criterion set out here, and recommended continuation of this randomization based on an observed difference in remission rates. Results from AML14 were kept blinded pending the completion of recruitment in AML16. Two options, (1) LDAC plus arsenic trioxide and (2) LDAC plus tipifarnib failed to pass the initial continuation hurdle and were consequently closed and reported.12,13 LDAC versus LDAC plus GO and LDAC versus clofarabine both passed the 2 interim analysis points and proceeded to a full trial of 400 patients. To replace arms that had closed, an evaluation of the nucleoside analog Sapacitabine was introduced in 2010.
Lessons learned from AML16 Pick a Winner
The illustration in Table 3 demonstrating the economy of the Pick a Winner design makes the assumption that all randomizations are open simultaneously and that all patients are randomized between all options. Under these circumstances, only 20% of patients randomized in AML16 would be allocated to receive LDAC. However, in this instance, arms opened at different times, not least because the LDAC plus arsenic trioxide and LDAC plus tipifarnib randomizations closed early. In addition, certain arms had particular eligibility criteria (such as hepatic function for GO and renal function for clofarabine), reducing the number of available arms for some patients. There was also a temporary preference to pick a randomization (eg, because it involved less hospitalization). Consequently, the recruitment was skewed overall toward LDAC, even though each individual comparison is in a 1:1 randomization. Another barrier to economy of patients occurred because the assessments by the DMEC were date driven rather than event driven. The decision was made to keep arms open until such time as the DMEC chose to close then, which resulted in more patients accruing to a particular randomization than would have been required if the review time point had been event driven. This clearly can be addressed by ensuring that DMEC meetings occur at the optimal event/recruitment-based time points, which would be helped by routine electronic data capture. In addition, especially if there are a number of novel treatment options, it would be possible to temporarily close a treatment arm and allow data to accumulate once sufficient patients have been recruited: there would still be sufficient open treatment arms to ensure that patient recruitment to the trial is not affected by this scenario.
As a result of our AML14 experience with LDAC, CR was adopted as a reliable surrogate for survival. Although this may be generally true, some reservations should be considered. Recent experience with the use of demethylation agents in AML suggests that survival improvement may not require the achievement of CR.14-16 Whether this is generally true for AML and delivers a better overall survival than LDAC remains to be shown. Under these circumstances, the flexibility of Pick a Winner is intact because the end point could be adjusted to early survival (based on a hazard ratio after a set number of events) rather than CR. Although, in general, achieving a CR is an indicator of survival benefit, this may not be the case. For example, the combination of LDAC plus GO doubled the CR rate but did not improve survival.17 This also presupposes that survival needs to be the ultimate end point in this older patient group, whereas a useful duration of CR might enhance the quality of life without extending it.
In some trials of conventional design and size, it has been possible to identify subsets of patients who preferentially benefit. Although this is less likely in the Pick a Winner design, the DMEC scrutiny may pick up a clue, which could subsequently be verified by continuing the assessment with eligibility limited to the subset. Similarly, where it is hypothesized that a subset will benefit (eg, from molecularly targeted therapy), then the eligibility could be set for that subpopulation alone.
Discussion
A major challenge in AML is the need to rapidly assess new treatments that have the potential to make clinically useful improvements. The Pick a Winner design provides a platform for exploring new treatments in a randomized fashion while allowing for early rejection of unpromising treatments. The necessity for randomization is illustrated by a consideration of the control remission rates in the different comparisons within AML16 and the AML14 GO comparison. In the AML14 GO randomization, the control remission rate was only 8%, whereas for one comparison in AML16 the control remission rate was 22%. This observation shows that an uncontrolled evaluation may well be misleading.
The economy of Pick a Winner is based on 2 tenets. By simultaneous randomization between a number of different novel therapies, there is a saving in the number of patients given control treatment. A further economic benefit would accrue to the trial funders on the basis that less resource is needed for a rolling trial program than a series of individual trials. However, the biggest potential economy in patient numbers arises from the potential for early rejection of unpromising treatments. Key to this is the assumption that small improvements in survival in this group of patients are not worthwhile. One approach to identifying the minimal clinically relevant benefit is accept the cost-effectiveness criteria as set out, for example, by bodies such as the National Institute for Health and Clinical Excellence in the United Kingdom. The commonly quoted upper National Institute for Health and Clinical Excellence guideline of £30 000 per quality-adjusted life year18 gives a rough measure of the clinically important difference required. Based on the shape of the curve in the first year and the expected duration of any treatment benefit, the minimum absolute survival benefit for a drug to pass the threshold can be calculated from the cost of the drug. Table 4 shows the results of such calculations for a variety of scenarios. The assumption made here is that any benefit seen at the end of the first year manifests itself as a gradual divergence of the survival curves, leading to an average life benefit in year 1 (area between the survival curves) of approximately half the absolute benefit at the end of year 1. The calculations are, however, relatively robust to the precise shape of the survival curves, especially as the benefit is predicted to persist for longer. From Table 4, it can be seen that, if a treatment costs £7500 then, if any survival benefit in year one persists for a further 2 years, the critical requirement is for a 10% improvement in survival. However, if the benefit is expected to persist only for a further 1 year, the required survival advantage increases to 17%. An additional feature is that more expensive drugs need to produce a long-term cure, as even with 3 years persistent benefit, a treatment costing £40 000 requires a 38% absolute survival benefit at the end of year 1. Although the National Institute for Health and Clinical Excellence criteria may be a special case, the inherent frailty of this patient population (as they are older and not deemed suitable for intensive chemotherapy) raises the question as to whether such expensive treatments can ever be sufficiently cost-effective in this population. Indeed, the values in Table 4 need to be discounted by any impact the novel treatment may have on quality of life, either long-term or during the treatment period.
Absolute improvements in 1-year survival required based on a threshold of £30 000 per life year
| Cost of treatment, £ . | Required 1-year absolute survival benefit if treatment benefit persists for indicated time . | |||
|---|---|---|---|---|
| 1 year, % . | 18 months, % . | 2 years, % . | 3 years, % . | |
| 2500 | 6 | 4 | 3 | 2 |
| 5000 | 11 | 8 | 7 | 5 |
| 7500 | 17 | 13 | 10 | 7 |
| 10 000 | 22 | 17 | 13 | 10 |
| 12 500 | 28 | 21 | 17 | 12 |
| 15 000 | 33 | 25 | 20 | 14 |
| 20 000 | 44 | 33 | 27 | 19 |
| 25 000 | 56 | 42 | 33 | 24 |
| 30 000 | 67 | 50 | 40 | 29 |
| 40 000 | 89 | 67 | 53 | 38 |
| Cost of treatment, £ . | Required 1-year absolute survival benefit if treatment benefit persists for indicated time . | |||
|---|---|---|---|---|
| 1 year, % . | 18 months, % . | 2 years, % . | 3 years, % . | |
| 2500 | 6 | 4 | 3 | 2 |
| 5000 | 11 | 8 | 7 | 5 |
| 7500 | 17 | 13 | 10 | 7 |
| 10 000 | 22 | 17 | 13 | 10 |
| 12 500 | 28 | 21 | 17 | 12 |
| 15 000 | 33 | 25 | 20 | 14 |
| 20 000 | 44 | 33 | 27 | 19 |
| 25 000 | 56 | 42 | 33 | 24 |
| 30 000 | 67 | 50 | 40 | 29 |
| 40 000 | 89 | 67 | 53 | 38 |
The table assumes an average extension of life in year 1 of half the end-of-year benefit, and that the benefit persists for 1, 1.5, 2, or 3 years beyond that.
Our experience with the NCRI AML16 trial clearly demonstrates that, in the situation of older patients with AML unfit for chemotherapy, the Pick a Winner design is both feasible and efficient, albeit with some further modifications to improve the operating characteristics of the trial. Indeed, recruitment in AML16 Pick a Winner has been 4 times as fast as was seen in the same nonintensive group in our previous trials. The trial provides a good illustration of what are effectively wider principles. Pick a Winner is efficient so long as the setting is one where an early assessment of outcome can be made and where small to moderate benefits are unlikely to be clinically worthwhile. Because the aim is to find a new standard of care, the flexibility must allow for the possibility that one of the test arms becomes a winner. Logically, this should become the new control arm. Although circumstances may permit this, commercial considerations would arise, especially if the drug did not have appropriate approval. In such circumstances, “doctor's choice” could be an alternative. However, if more than one test arm were simultaneously to beat the standard of care, this design would not be able precisely to define the best option as it is not set up to perform head-to-head comparisons between novel agents. In addition, the magnitude of such differences may well be smaller than between novel treatments and standard of care, and a larger trial would probably be needed at this point.
Finally, this approach requires close collaboration between academia and the pharmaceutical industry, with the probability that it could only be undertaken in the academic setting because of commercial sensitivities. However, there are a number of situations both in hematology and beyond which could benefit from a Pick a Winner approach. Bearing in mind the requirements set out in Table 1, a frequent early surrogate end point is a prerequisite. In younger patients with AML, the setting of induction and consolidation is unlikely to be productive. Induction differences would require a substantial number of patients, and consolidation would in addition need significant periods of follow-up. However, a case could be made for patients with relapsed, refractory or high-risk disease. Minimal residual disease could be a suitable early surrogate end point that could be useful in AML, chronic lymphatic leukemia, or myeloma that has failed first line therapy. With the rise in so-called therapy acceleration programs (designed to shorten the time between bench and bedside for new treatments), it has become clear that progress requires tackling the bottleneck in drug development at the point of testing treatments in patients in phase 1b/2 trials. The additional concept of drug X enables a program of continuous assessment by introducing new options by protocol amendment rather than freestanding separate trials, which dramatically reduces implementation time, cost, and administrative hurdles.
Acknowledgments
The authors thank Prof Keith Wheatley, University of Birmingham, for comments, Dr Laura Buckley for helping to run some of the computer simulations programmed by R.K.H., and Prof Elihu Estey for comments on an earlier draft of the manuscript.
The concept of the Pick a Winner design is based on work performed by Professors P. Royston and M. Parmar of the Medical Research Council Clinical Trials Unit, London.
Authorship
Contribution: A.K.B. devised the concept and wrote the paper; and R.K.H. undertook the mathematical and statistical calculations and wrote the paper.
Conflict-of-interest disclosure: The authors declare no competing financial interests.
Correspondence: Robert K. Hills, Department of Haematology, Cardiff University School of Medicine, Heath Park, Cardiff CF14 4XN, United Kingdom; e-mail: HillsRK@cf.ac.uk.