Abstract
Disruption of spectrin self-association underlies many inherited hemolytic disorders. Using dynamic modeling and energy minimization, the 3-dimensional structure of the self-association domain has been estimated in human erythrocyte spectrin and the structural consequences of 17 elliptogenic mutations determined. The predicted structure of the normal self-association domain was remarkably similar to the crystal structure of the Drosophila α-spectrin 14th repeat unit, despite replacement in the human sequence of over 70% of the amino acids relative to fly spectrin, including 2 prolines in the human sequence that appear in helical regions of the fly structure. The predicted structure placed all hydrophilic residues at the surface and identified 4 salt bridges, 9 hydrophobic interactions, and 4 H-bonds that stabilize the native self-association unit. Remarkably, every pathologic point mutation, including seemingly conservative substitutions such as G for A, A for V, or K for R (single-letter amino acid codes), led to conformational rearrangements in the predicted structure. The degree of structural disruption, as measured by root-mean-square deviation of the predicted backbone structure from theDrosophila structure, correlated strongly with the severity of clinical disease associated with each mutation. This approach thus enables an accurate prediction, from the primary sequence, of the clinical consequences of specific point mutations in spectrin. The 3-dimensional structure of the self-association domain derived here is likely to be accurate. It provides a powerful heuristic model for understanding how point mutations disrupt cytoskeletal function in a variety of hemolytic disorders.
Introduction
The shape and stability of the human erythrocyte derives from a delicately balanced surface area–volume ratio and the lateral distribution and abundance of its integral membrane proteins, as modified by their attachment to an underlying spectrin-actin skeleton.1-4 Although the energetics of the membrane may be dominated by interactions of integral proteins within the bilayer,5 the homogeneous spectrin skeleton modifies cell stability by modifying bilayer elasticity, by tethering or trapping membrane proteins so as to limit their lateral diffusability and ensure their quasi-random distribution, and by dampening the rate of protein rearrangement during cyclic cell deformation (as occurs during capillary passage).
One pathway by which the energetics of elasticity and membrane protein-distribution control can be altered is by failure of the spectrin skeleton to adequately form an anastamosing meshwork beneath the membrane, usually due to failures in self-association. Such disorders typically lead to asymmetrical distortions in the shape and deformability of the red blood cell (RBC), as in various forms of hereditary elliptocytosis (HE) (reviewed in Morrow et al,2Tse and Lux,3 Delaunay and Dhermy,6 and Gallagher and Jarolim7). Spectrin itself is composed of a heterodimer of 2 structurally similar proteins, α- and β-spectrin,2,8 encoded by separate genes.9,10 Spectrin heterodimers self-associate in an end-on fashion to form tetramers and higher order oligomers (Figure1).11,12 This oligomerization is critical for erythrocyte membrane stability as well as erythrocyte shape and function. The first recognition that mutations in spectrin that impair its ability to self-associate lead to clinically significant forms of HE and hereditary pyropoikilocytosis (HPP) came from the study of a small family with 2 severely afflicted siblings who displayed bizarre misshapen RBCs (poikilocytes), and with an older sibling and mother who displayed less severe disease with elliptocytic RBCs.13 14 Subsequent studies in many laboratories examining other patients with HE and HPP have identified a number of hereditary conditions characterized by point mutations that reduce the self-association ability of spectrin.
Cartoon of the self-association site of spectrin.
The self-association site is formed by a contribution of one helix from the amino-terminus of α-spectrin, and 2 helices from the incomplete 17th repeat unit near the COOH-terminus of β-spectrin.
Cartoon of the self-association site of spectrin.
The self-association site is formed by a contribution of one helix from the amino-terminus of α-spectrin, and 2 helices from the incomplete 17th repeat unit near the COOH-terminus of β-spectrin.
Although the realization that point mutations in spectrin can cause hemolytic disease opened a new era of understanding and nosology of these disorders,15 there has been little progress in understanding how such mutations actually perturb the function of spectrin. Insightful analyses based on the complete sequence of spectrin revealed that spectrin is composed of repeats of ≈106 amino acids, and suggested that these repeats fold into α-helical, coiled-coil triple helices.9,10,16 In these putative repeats, the first and third helices were envisioned to be parallel and the second helix antiparallel. Support for this model has been provided by x-ray, nuclear magnetic resonance (NMR), and spectroscopic studies of spectrin.17-23 The spectrin triple helical repeats are amphipathic and stabilized by the sequestration of the hydrophobic faces of each helix along the interior of the repeat bundle. Phasing of the repeats revealed that there are incomplete repeats at the NH2-terminus of α-spectrin and the COOH-terminus of β-spectrin (by 1 and 2 helices, respectively). When a point mutation was identified in the COOH-terminal partial repeat of β-spectrin from an HE/HPP kindred with severe anemia and impaired spectrin self-association, it was postulated that the self-association site in spectrin must be formed from an atypical triple helical unit involving the interaction of the COOH-terminus of β-spectrin (helices A and B) and the NH2-terminus of α-spectrin (helix C) (Figure 1, bottom).24 Additional studies have identified over 20 mutations associated with HE or HPP in this atypical triple helical unit that are defective in spectrin self-association (Table1). Other work detected further correlations between the clinical HE/HPP phenotype and the presence of mutations in this putative triple helical unit.6,25Studies examining directly the self-association activity of spectrin using recombinant peptides also came to a similar conclusion,26-29 and have demonstrated that this atypical repeat forms the critical region of the spectrin self-association site.
Positions of point mutations in the spectrin self-association domain
| Codon . | Position in 106 residue repeat . | Amino acid . | Mutant . | Comment . | RMSΔ* (Å) . | Clinical severity . | Reference . |
|---|---|---|---|---|---|---|---|
| β-Spectrin | |||||||
| 2018 | 11 | A | G | Spectrin Cagliari | 4.5729 | 2 | 43 |
| 2019 | 12 | S | P | Spectrin Providence | 4.4747 | 3 | 37 |
| 2023 | 16 | A | V | 4.9564 | 3 | 44 | |
| 2024 | 17 | W | R | 3.3006 | 2 | 44 | |
| 2025 | 18 | L | R | Spectrin Buffalo | 4.9359 | 3 | 42 |
| 2053 | 46 | A | P | 4.3999 | 3 | 24 | |
| 2061 | 54 | W | R | ND | 2 | 25,45 | |
| 2064 | 57 | R | P | Spectrin Cosenza | ND | 2 | 46 |
| α-Spectrin | |||||||
| 24 | 79 | I | S | 2.8271 | 1 | 44 | |
| 28 | 83 | R | H | Spectrin Tunisia | 5.3170 | 3 | 38, 47-49 |
| 28 | 83 | R | S | 6.2351 | 4 | 48, 50 | |
| 28 | 83 | R | L | 10.0354 | 4 | 48, 50 | |
| 28 | 83 | R | C | 5.1409 | 3 | 48, 51 | |
| 34 | 89 | R | W | Spectrin Genova | 3.7954 | 2 | 52 |
| 41 | 96 | R | W | Spectrin Tunis | 3.1034 | 1 | 53 |
| 45 | 100 | R | S | 3.1557 | 2 | 54 | |
| 45 | 100 | R | T | Spectrin Anastasia | ND | 1 | 55 |
| 46 | 101 | G | V | Spectrin Culoz | 4.7368 | 3 | 56 |
| 48 | 103 | K | R | 2.4822 | 0 | 50 | |
| 49 | 104 | L | F | Spectrin Lyon | 3.1990 | 1 | 56 |
| Codon . | Position in 106 residue repeat . | Amino acid . | Mutant . | Comment . | RMSΔ* (Å) . | Clinical severity . | Reference . |
|---|---|---|---|---|---|---|---|
| β-Spectrin | |||||||
| 2018 | 11 | A | G | Spectrin Cagliari | 4.5729 | 2 | 43 |
| 2019 | 12 | S | P | Spectrin Providence | 4.4747 | 3 | 37 |
| 2023 | 16 | A | V | 4.9564 | 3 | 44 | |
| 2024 | 17 | W | R | 3.3006 | 2 | 44 | |
| 2025 | 18 | L | R | Spectrin Buffalo | 4.9359 | 3 | 42 |
| 2053 | 46 | A | P | 4.3999 | 3 | 24 | |
| 2061 | 54 | W | R | ND | 2 | 25,45 | |
| 2064 | 57 | R | P | Spectrin Cosenza | ND | 2 | 46 |
| α-Spectrin | |||||||
| 24 | 79 | I | S | 2.8271 | 1 | 44 | |
| 28 | 83 | R | H | Spectrin Tunisia | 5.3170 | 3 | 38, 47-49 |
| 28 | 83 | R | S | 6.2351 | 4 | 48, 50 | |
| 28 | 83 | R | L | 10.0354 | 4 | 48, 50 | |
| 28 | 83 | R | C | 5.1409 | 3 | 48, 51 | |
| 34 | 89 | R | W | Spectrin Genova | 3.7954 | 2 | 52 |
| 41 | 96 | R | W | Spectrin Tunis | 3.1034 | 1 | 53 |
| 45 | 100 | R | S | 3.1557 | 2 | 54 | |
| 45 | 100 | R | T | Spectrin Anastasia | ND | 1 | 55 |
| 46 | 101 | G | V | Spectrin Culoz | 4.7368 | 3 | 56 |
| 48 | 103 | K | R | 2.4822 | 0 | 50 | |
| 49 | 104 | L | F | Spectrin Lyon | 3.1990 | 1 | 56 |
Root-mean square deviation of the predicted backbone structure compared to the Drosophila 14th repeat crystal structure, as reported by Yan and colleagues.17 The fit for the wild-type Drosophila sequence = 1.9897 Å; wild-type (normal) human = 2.8457 Å.
Despite these advances, the challenge of understanding in detail the structure of the spectrin self-association domain remains. Given the lability and low-affinity of this noncovalent interaction (Ka ≈10 μM), the direct resolution of its structure by either multidimensional NMR or crystallography is a daunting challenge. As an alternative, we have explored the power of computational strategies to develop plausible models of this dynamic structure. These efforts involve the conceptual folding of 2 peptide sequences representing the self-association domains of α- and β-spectrin.26 27 This modeling seeks to minimize the total system energy derived from all backbone and side-chain interactions, including interactions with a surrounding hydration shell. Dynamic modeling is used to facilitate the refinement of the structure and to relieve forbidden steric or angular dependencies. The resultant structures are triple helical, and for wild-type sequences are closely similar to the crystal structures of a single spectrin repeat unit. Interestingly, we find that even ostensibly conservative single residue replacements can significantly destabilize the predicted structure, with the degree of destabilization closely paralleling the clinical severity associated with each mutation.
Materials and methods
Molecular modeling
Programs used to calculate the total system energy of different conformations, and to present the resultant structures as 3-dimensional representations, included X-plor, version 3.1m,31 and the program Insight32; both were operated on a Silicon Graphics Indigo2 Extreme workstation. The starting structure for the modeling was that portion of the crystal structure ofDrosophila spectrin that represents a single repeat unit.17 The 2-repeat triple helical crystal structure of chicken α-spectrin23 was also considered as a starting point for the modeling determinations, but was deemed to be less suitable because it shared a backbone structure that was almost indistinguishable from the fly (root-mean-square deviation [RMSΔ] = 1.98 Å); was less well resolved relative to the fly structure (2.0 Å versus 1.8 Å); and surprisingly, shared less primary sequence homology with the putative human self-association domain than did the Drosophila sequence (25%-30% homology for avian spectrin versus 33% for the fly 14th repeat). No attempts were made to model a structure based on the alternatively phased conformation of the avian 2-repeat structure,23 because this conformation was deemed to be an unlikely candidate given the absence of covalent continuity between the putative B and C helices of the self-association site (see below), continuity that would a priori appear to be a prerequisite to extend the B helix at the expense of the C helix in this conformation. To establish the validity of the modeling simulations and to explore the parameters needed to achieve a creditable approximation, the structure of the Drosophilaα-spectrin 14th structural repeat itself was modeled and compared with its crystal structure. The molecular dynamics at 300°K of theDrosophila α-spectrin 14th repeat were initially modeled in a vacuum, using the Verlet method.33 This approach yielded helices at the NH2- and COOH-termini that unwound excessively, and the orientation of the amino acid side chains were dissimilar to the crystal structure. This same result was obtained when a simulated annealing starting at high temperature was used. These results suggested that simulation in a vacuum was inappropriate for this super helix of the 3 helices, and suggested that interactions between spectrin and the aqueous environment were critical to its structure. To solve this problem, and given practical limitations on the computational complexity that could be managed, the effects of modeling this structure in a 6-Å water shell using both molecular dynamics at 300°K and simulated annealing from high temperatures were evaluated. The starting structure was “placed” in a 6-Å-thick water shell that contained about 1100 water molecules. Five hundred steps of Powell conjugate gradient energy minimization34were first performed to minimize the system energy. Then Verlet molecular dynamics was used to accomplish the simulated annealing. The simulated temperature was raised to 1000°K, and then cooled to 110°K in steps of 10°K. At each temperature, 400 time-steps of dynamic calculation were performed. Time-step increments (TSk) were determined by the following formula:
The total simulation time was 16.5 picoseconds (ps). The initial velocity was randomly set according the Maxwell velocity distribution. The frictional coefficient was set to 100 ps−1 for all atoms. A structure was sampled after each temperature step. The 90 sampled structures were energy minimized by the Powell conjugate gradient energy minimization with 2000 steps, and the 10 structures with lowest energy minima were averaged. Energy minimization was then again performed on the averaged structure with 2000 steps. The tolerance for the norm of the gradient of Etotal was 0.01 during all of the energy minimization procedures. This approach yielded better agreement with the known crystal structure (described below and Figure 2).
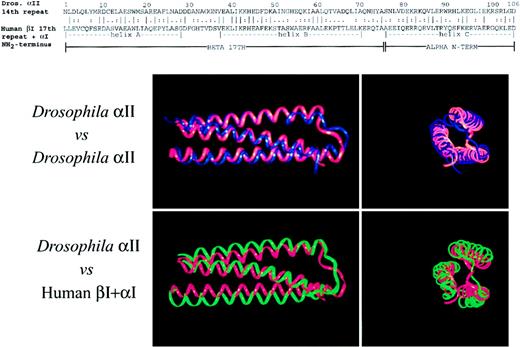
The self-association domain of spectrin can be modeled as a triple helix.
(Top) Alignment of the primary sequence of Drosophilaα-spectrin 14th unit with the partial repeat units from the amino-terminus of human αΙ-spectrin (residues 19-51) and from the 17th repeat unit of βΙ-spectrin (residues 2008-2080), using the program Bestfit.35 The position of the 3 helices as determined from the crystal structure of the Drosophilaspectrin are shown. Continuity was not assumed where the 2 subunits join in the concatenated sequence. This concatenated sequence, with or without the mutations described in the text, was then treated as a pseudo-106 residue repeat unit for the dynamic modeling studies. Dros indicates Drosophila; term, terminus. (Bottom) Comparison of the calculated structure of Drosophila α-spectrin 14th repeat (blue) or the concatenated human αΙβΙ self-association domain (green) with the crystal structure of the Drosophila14th repeat (red). Two views are shown, longitudinal on the left, and an end-on view on the right. The 6-Å hydration shell involving 1100 water molecules is not shown. This hydration shell is required for the predicted structure to fold to a triple-helical unit. Note the close correspondence of the fitted structures with the crystal, even though in the case of the self-association domain, 70% of the residues differ from those in the Drosophila protein.
The self-association domain of spectrin can be modeled as a triple helix.
(Top) Alignment of the primary sequence of Drosophilaα-spectrin 14th unit with the partial repeat units from the amino-terminus of human αΙ-spectrin (residues 19-51) and from the 17th repeat unit of βΙ-spectrin (residues 2008-2080), using the program Bestfit.35 The position of the 3 helices as determined from the crystal structure of the Drosophilaspectrin are shown. Continuity was not assumed where the 2 subunits join in the concatenated sequence. This concatenated sequence, with or without the mutations described in the text, was then treated as a pseudo-106 residue repeat unit for the dynamic modeling studies. Dros indicates Drosophila; term, terminus. (Bottom) Comparison of the calculated structure of Drosophila α-spectrin 14th repeat (blue) or the concatenated human αΙβΙ self-association domain (green) with the crystal structure of the Drosophila14th repeat (red). Two views are shown, longitudinal on the left, and an end-on view on the right. The 6-Å hydration shell involving 1100 water molecules is not shown. This hydration shell is required for the predicted structure to fold to a triple-helical unit. Note the close correspondence of the fitted structures with the crystal, even though in the case of the self-association domain, 70% of the residues differ from those in the Drosophila protein.
Alignment of the structural unit with the self-association domain
For purposes of molecular modeling, the self-association domain of αΙβΙ spectrin was evaluated as a single concatenated sequence. To approximate the positioning of the putative triple helical self-association unit relative to the Drosophila structural repeat, the sequence of the self-association unit of αΙβΙ-spectrin was aligned with the 14th repeat unit ofDrosophila α-spectrin using the program BestFit35 (Figure 2, top). The corresponding residues of human spectrin were then graphically incorporated into the published crystallographic coordinates of fly spectrin, thereby creating astarting structure for the dynamic modeling computations. Residues 1 to 73 of the α chain in the Drosophila crystal structure were replaced with the partial 17th structural unit of βΙ-spectrin. Residues 74 to 106 of the crystal structure were replaced with the extended amino-terminus of αΙ-spectrin. A pseudo repeat unit with a continuous peptide chain was thus generated for use in the modeling calculations (although to faithfully reflect the native state, the calculations did not assume continuity between the α- and β-spectrin concatenated sequences). A total of 73 residues were substituted relative to the Drosophila sequence for the wild-type self-association domain, and 72 + 1 (mutant) residues for each mutant examined. Replaced structures were used as the starting structure for the molecular modeling algorithms. It is noteworthy that many of the replaced residues even in the wild-type spectrin represent nonconservative substitutions relative to theDrosophila sequence, including the inclusion of a proline residue in the middle of helix C. Yet, and despite these many substitutions, the modeling algorithms converged on a predicted structure for the normal human self-association domain that was remarkably similar in its overall structural features to theDrosophila structure unit (Figure 2, bottom).
Determination of side-chain interactions
Salt-bridge interactions and hydrophobic interactions between residues were scored as positive if they fell within 5 Å of each other in the refined structure. Hydrogen bonds were scored as present if the distance between the electronegative atoms (N & O) within O-H-N or O-H-O groups were ≈2.9 Å apart.
Evaluation of clinical severity
In evaluating the clinical impact of each spectrin mutation, consideration was given to the degree of hemolysis or RBC cell fragility, steady-state hemoglobin or hematocrit (in nontransfused subjects), the reticulocyte count, transfusion dependency, whether splenectomy had been necessary, the degree of morphologic abnormality, and the overall morbidity and mortality. These parameters were extracted from clinical data described in the original reports (Table1). Patients with no abnormalities in erythrocyte shape or stability were scored 0; shape abnormalities without evidence of hemolysis or clinical disease were +1; mild hemolysis but not requiring splenectomy, +2; severe hemolysis with or without splenectomy, possibly lethal in homozygous state, +3; and the most severe disease, transfusion dependent, always lethal in homozygotes, +4.
Results
Molecular modeling predicts a plausible model of the spectrin self-association domain
The simulated structure of the 14th structural unit ofDrosophila α-spectrin derived by this method was superimposed onto its crystal structure (Figure 2, bottom). As noted in a previous study using a similar approach,36 the predicted structure, including the orientation of the side chains, agrees well with the crystal structure. The RMSΔ for the comparison between the crystal structure and that estimated by the above modeling procedure for Drosophila α-spectrin was 1.99 Å for the backbone atoms and 2.42 Å for all heavy atoms. Overall, the calculated structure is a bit less compact compared to the crystal structure. It is not known if this small difference represents errors in the computational approximation or a real difference in compactness between the solution structure and that of the crystal (which is prepared but not modeled in a high-salt environment).
The predicted structure for the normal spectrin self-association domain is also similar to the structure of the Drosophila repeat, with a backbone RMSΔ of just 2.846Å (Figure 2). This is a satisfactory result, given that over 70% of the structure has been replaced with different amino acids, including 2 proline residues at positions 23 in helix A and 64 in helix B (β-spectrin residues 2030 and 2071, respectively). It is also important to note that the similarity of the predicted normal human self-association unit to theDrosophila structural repeat is unlikely to reflect an insensitivity of the modeling algorithms to the variant sequences, because as demonstrated below, single residue replacements that are known to affect the function of the self-association domain have a profound effect on the predicted structure.
Interactions of helix C with helices A and B primarily stabilize the self-association unit
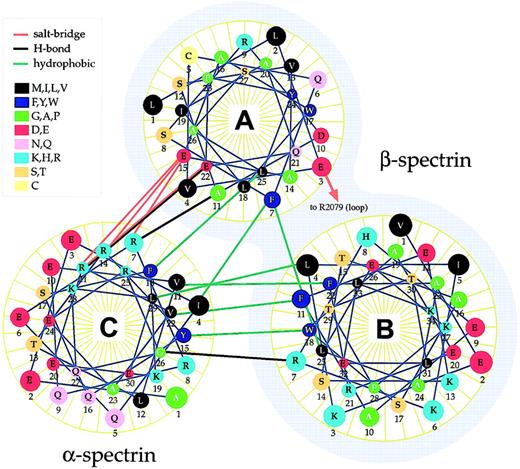
Based on the plausibility of the predicted overall tertiary and quaternary structure of the self-association unit, an analysis was carried out to identify interactions predicted to maximally stabilize the functional unit (as described in “Materials and methods”). Three types of linkages were evaluated: hydrophobic interactions involving nonpolar side chains; hydrogen bonds, and ionic charge interactions (salt bridges). These results are summarized in Figure3 and Table2. Interestingly, most of the putative strong interactions identified in the modeled structure involve helix C interacting with helix A or B. Just 2 direct interactions were predicted between helices A and B, and one of these is marginal (internuclear distance > 5 Å), suggesting that in the absence of a third helix (ie, the helix provided by α-spectrin), the self-association domain probably exists in a more open conformation with its 2 helices at least partially extended. This prediction is consonant with the intermediate open state identified in studies examining the protease-resistant structure of β-spectrin.26
Helical wheel depiction of the self-association unit.
The predicted structure of the normal spectrin self-association unit was examined for the presence of various types of noncovalent interactions, based on their chemical characteristics and proximity. These interactions are depicted and are summarized in Table 2. Note that nearly all of the interactions stabilizing the triple helical self-association unit arise between helix A or B with helix C. One interaction between helix A and B involves a salt bridge with R2079 (labeled), which falls in the loop sequence between helix B and C. Helices A and B are derived from β-spectrin (shaded), helix C from α-spectrin.
Helical wheel depiction of the self-association unit.
The predicted structure of the normal spectrin self-association unit was examined for the presence of various types of noncovalent interactions, based on their chemical characteristics and proximity. These interactions are depicted and are summarized in Table 2. Note that nearly all of the interactions stabilizing the triple helical self-association unit arise between helix A or B with helix C. One interaction between helix A and B involves a salt bridge with R2079 (labeled), which falls in the loop sequence between helix B and C. Helices A and B are derived from β-spectrin (shaded), helix C from α-spectrin.
Side-chain interactions in the putative spectrin self-association domain
| Position in helix and residue . | Position in 106–amino acid motif . | Codon . | Interaction distance (Å)*,† . | Position in helix and residue . | Position in 106 amino acid motif . | Codon . | Interaction type . |
|---|---|---|---|---|---|---|---|
| Interacting residues between helix B and helix C | |||||||
| B7-R | 43 | 2055 | 3.04 | C26-G | 101 | 46 | H-bond (±) |
| B22-F | 58 | 2070 | 4.93 | C11-V | 86 | 31 | Hydrophobic |
| B18-W | 54 | 2066 | 3.52 | C15-Y | 90 | 35 | Hydrophobic |
| B18-W | 54 | 2066 | 3.50 | C18-F | 93 | 38 | Hydrophobic |
| B11-F | 47 | 2059 | 3.15 | C22-V | 97 | 42 | Hydrophobic |
| B11-F | 47 | 2059 | 4.57 | C23-A | 98 | 43 | Hydrophobic |
| B4-L | 40 | 2052 | 3.41 | C29-L | 104 | 49 | Hydrophobic |
| Interacting residues between helix A and helix C | |||||||
| A11-A | 11 | 2018 | 2.76 | C7-R | 82 | 28 | H-bond |
| A15-E | 15 | 2022 | 3.04 | C7-R | 82 | 28 | H-bond (±) |
| A22-E | 22 | 2029 | 2.79 | C21-R | 96 | 41 | H-bond |
| A7-F | 7 | 2014 | 4.07 | C4-I | 79 | 24 | Hydrophobic |
| A25-L | 25 | 2032 | 3.74 | C18-F | 93 | 38 | Hydrophobic |
| A15-E | 15 | 2022 | 3.81 | C7-R | 82 | 27 | Salt bridge |
| A15-E | 15 | 2022 | 4.94 | C14-R | 89 | 34 | Salt bridge |
| A22-E | 22 | 2029 | 4.53 | C21-R | 96 | 41 | Salt bridge |
| Interacting residues between helix A and helix B | |||||||
| A3-E | 3 | 2010 | 4.68 | B36-R | 72 | 2079 | Salt bridge |
| A7-F | 7 | 2014 | 5.35 | B25-L | 61 | 2068 | Hydrophobic (±) |
| Position in helix and residue . | Position in 106–amino acid motif . | Codon . | Interaction distance (Å)*,† . | Position in helix and residue . | Position in 106 amino acid motif . | Codon . | Interaction type . |
|---|---|---|---|---|---|---|---|
| Interacting residues between helix B and helix C | |||||||
| B7-R | 43 | 2055 | 3.04 | C26-G | 101 | 46 | H-bond (±) |
| B22-F | 58 | 2070 | 4.93 | C11-V | 86 | 31 | Hydrophobic |
| B18-W | 54 | 2066 | 3.52 | C15-Y | 90 | 35 | Hydrophobic |
| B18-W | 54 | 2066 | 3.50 | C18-F | 93 | 38 | Hydrophobic |
| B11-F | 47 | 2059 | 3.15 | C22-V | 97 | 42 | Hydrophobic |
| B11-F | 47 | 2059 | 4.57 | C23-A | 98 | 43 | Hydrophobic |
| B4-L | 40 | 2052 | 3.41 | C29-L | 104 | 49 | Hydrophobic |
| Interacting residues between helix A and helix C | |||||||
| A11-A | 11 | 2018 | 2.76 | C7-R | 82 | 28 | H-bond |
| A15-E | 15 | 2022 | 3.04 | C7-R | 82 | 28 | H-bond (±) |
| A22-E | 22 | 2029 | 2.79 | C21-R | 96 | 41 | H-bond |
| A7-F | 7 | 2014 | 4.07 | C4-I | 79 | 24 | Hydrophobic |
| A25-L | 25 | 2032 | 3.74 | C18-F | 93 | 38 | Hydrophobic |
| A15-E | 15 | 2022 | 3.81 | C7-R | 82 | 27 | Salt bridge |
| A15-E | 15 | 2022 | 4.94 | C14-R | 89 | 34 | Salt bridge |
| A22-E | 22 | 2029 | 4.53 | C21-R | 96 | 41 | Salt bridge |
| Interacting residues between helix A and helix B | |||||||
| A3-E | 3 | 2010 | 4.68 | B36-R | 72 | 2079 | Salt bridge |
| A7-F | 7 | 2014 | 5.35 | B25-L | 61 | 2068 | Hydrophobic (±) |
Distances for hydrophobic interactions were calculated from the 2 closest atoms of the interacting pair.
Distances for salt bridges were calculated from center-to-center of each salt charge in the pair.
Mutations of α- and β-spectrin destabilize the self-association domain
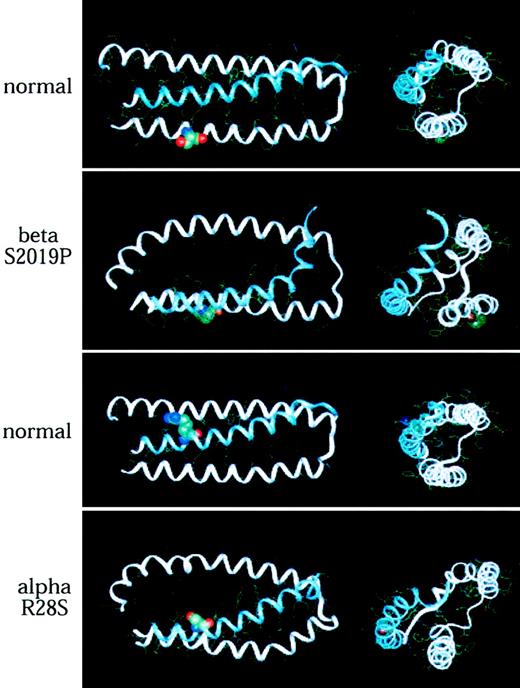
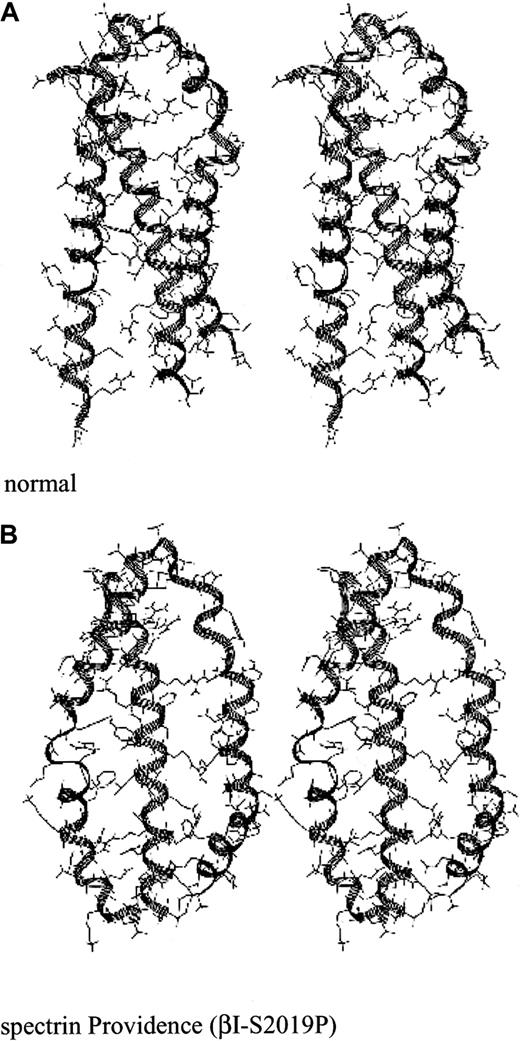
Spectrin Providence was first identified in a family with recurrent fatal erythroblastosis fetalis. The cause was traced to a P for S (single-letter amino acid codes) mutation at codon 2019 of β-spectrin. This residue falls in the middle of helix A. In the heterozygous state, these patients display elliptocytosis and marked erythrocyte fragility. Biochemical studies have established a substantial loss of self-association ability in this spectrin mutation. The predicted structural consequences of this mutation are profound (Figure 4, top, and Figure5). This single amino acid mutation leads the modeling algorithms to predict a markedly disrupted tertiary structure, with a splaying of helices A and B, and a loss of the narrow pocket into which helix C (α-spectrin) normally docks. Based on this predicted structure, it is hard to imagine how an effective self-association interaction could be achieved. These results fit well the measured self-association constant for this spectrin, which is more than 2 logs weaker than for normal spectrin.37 The severe disruption of the self-association domain that follows the Providence mutation can be better appreciated in the stereo presentation (Figure 5).
Mutations of α- and β-spectrin disrupt the normal predicted structure of the spectrin self-association domain.
(Top pair) Structure of normal spectrin versus spectrin Providence, showing the position of the S→P amino acid replacement at codon β2019 (position 12 in the A helix). Note the predicted severe distortion of this helix, with loss of the β-spectrin pocket into which α-spectrin (helix C) docks. (Bottom pair) A similar analysis revealing the predicted effect of a mutation in codon 28 of α-spectrin (R28S), a mutation that leads to hereditary pyropoikilocytosis. Even though the serine in this mutation is hydrophilic like the residue it replaces (R), the loss of the 2 putative salt bridges formed by the lost arginine (Table 2) destabilizes the self-association binding site. In each model, longitudinal and end-on views are shown. The mutated residue is depicted in space-filled form.
Mutations of α- and β-spectrin disrupt the normal predicted structure of the spectrin self-association domain.
(Top pair) Structure of normal spectrin versus spectrin Providence, showing the position of the S→P amino acid replacement at codon β2019 (position 12 in the A helix). Note the predicted severe distortion of this helix, with loss of the β-spectrin pocket into which α-spectrin (helix C) docks. (Bottom pair) A similar analysis revealing the predicted effect of a mutation in codon 28 of α-spectrin (R28S), a mutation that leads to hereditary pyropoikilocytosis. Even though the serine in this mutation is hydrophilic like the residue it replaces (R), the loss of the 2 putative salt bridges formed by the lost arginine (Table 2) destabilizes the self-association binding site. In each model, longitudinal and end-on views are shown. The mutated residue is depicted in space-filled form.
Stereo drawing of the spectrin Providence mutation.
(A) Predicted structure of the normal self-association unit. (B) Predicted structure of the self-association unit in spectrin Providence. This spectrin mutation leads to severe hemolytic disease and erythroblastosis fetalis in the homozygous state.37
Stereo drawing of the spectrin Providence mutation.
(A) Predicted structure of the normal self-association unit. (B) Predicted structure of the self-association unit in spectrin Providence. This spectrin mutation leads to severe hemolytic disease and erythroblastosis fetalis in the homozygous state.37
Another site of mutation that commonly causes hemolytic disease is at codon 28 of αΙ-spectrin (Table 1). The predicted structure of spectrin with an R→S mutation at this locus is shown (Figure 4, bottom). Given that both S and R are hydrophilic, it is surprising that this substitution would have such dramatic structural consequences. Similarly, spectrin Corbeil, an R→H mutation at this locus, is also associated with significant poikilocytic hemolytic anemia and defective spectrin self-association.38 The model of spectrin Corbeil (Figure 6) also predicts major conformational changes. Given that α28 is the codon most commonly mutated in HE and HPP, it is gratifying that these modeling studies reveal it to be critical for maintaining the secondary, tertiary, and quaternary structure of the self-association unit. Indeed, even ostensibly conservative substitutions at this locus (such as R→H) are disruptive. Presumably, this sensitivity reflects the requirement for the 2 hydrogen bonds formed between R28 and residues 2018 and 2022 of β-spectrin.
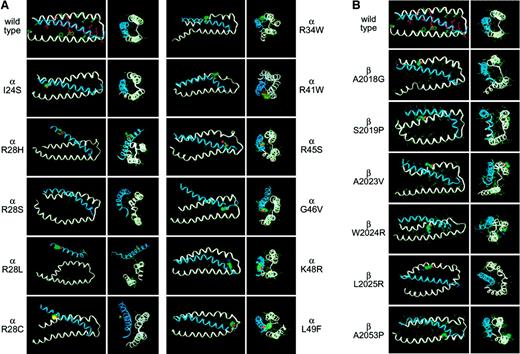
Modeling of 17 pathogenic mutations in the spectrin self-association domain.
(A) Mutations involving αΙ-spectrin. (B) Mutations involving βΙ-spectrin. Note the predicted disruption, sometimes severe, that accompanies the substitution of even a single native residue. Longitudinal and end-on views are shown for each mutation. The mutated residue is depicted in each case using a solid-filled representation. The coordinates for each of these modeled structures are available as .PDB files (downloadable as .RTF files) on the Blood website as supplemental material; see the Supplemental Data Sets link at the top of the online article.
Modeling of 17 pathogenic mutations in the spectrin self-association domain.
(A) Mutations involving αΙ-spectrin. (B) Mutations involving βΙ-spectrin. Note the predicted disruption, sometimes severe, that accompanies the substitution of even a single native residue. Longitudinal and end-on views are shown for each mutation. The mutated residue is depicted in each case using a solid-filled representation. The coordinates for each of these modeled structures are available as .PDB files (downloadable as .RTF files) on the Blood website as supplemental material; see the Supplemental Data Sets link at the top of the online article.
All pathogenic mutations disrupt the predicted tertiary structure of the self-association domain
To establish the generality and predictive value of the modeling algorithm, 17 different mutations involving either the α- or β-subunit of spectrin were modeled. All of these mutations have been identified because they generate a detectable phenotype. The severity of these phenotypes ranges from severe and often fatal hemolytic anemias or erythroblastosis fetalis to minor disturbances in erythrocyte shape without measurable disturbances in stability. These mutations are summarized in Table 1, and the derived structures are shown in Figure 6. It is apparent that for all pathologic mutations, there is some disruption of the secondary, tertiary, and quaternary structure. The RMSΔ values of these structures relative to the crystal structure of Drosophila α-spectrin range from a value equivalent to the native structure (K28R αΙ-spectrin) to the markedly deviant structure predicted for the R28L mutation in αΙ-spectrin.
Molecular modeling correlates well with the clinical severity of each mutation
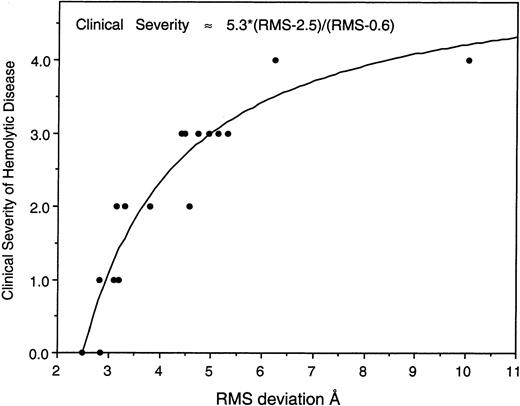
When the degree of predicted disruption in the structure of the self-association unit, as measured by the RMSΔ of its predicted backbone structure versus the Drosophila crystal structure, is compared to the approximate clinical severity of patients carrying the mutation, a striking correlation emerges (Figure7). Although this correlation must of necessity be only approximate, given the clinical heterogeneity observed for any given mutation even within the same family (eg, due to the presence of a low expression spectrin allele in cis ortrans),39 these findings strongly imply that the structural changes anticipated by the modeling algorithms are directly reflected in the functional integrity of the self-association domain.
The degree of predicted structural disruption correlates well with the clinical severity induced by the mutation.
For each of the 17 mutations in the self-association domain that were modeled (Table 1), the RMSΔ of their backbone structure versus that of the Drosophila crystal structure was plotted versus an estimate of the clinical severity of the condition, on a scale of 0 to 4 (as described in “Materials and methods”). Also included in this plot is the RMSΔ value for the native structure (2.846 Å, clinical severity = 0). Note that the deviation of the mutant structures, as predicted by dynamic molecular modeling from a knowledge of the primary sequence and the crystal structure of Drosophila spectrin, correlates well with the clinical severity of each mutation. This behavior can be approximated by the equation shown, derived by a nonlinear least squares fit to the data.
The degree of predicted structural disruption correlates well with the clinical severity induced by the mutation.
For each of the 17 mutations in the self-association domain that were modeled (Table 1), the RMSΔ of their backbone structure versus that of the Drosophila crystal structure was plotted versus an estimate of the clinical severity of the condition, on a scale of 0 to 4 (as described in “Materials and methods”). Also included in this plot is the RMSΔ value for the native structure (2.846 Å, clinical severity = 0). Note that the deviation of the mutant structures, as predicted by dynamic molecular modeling from a knowledge of the primary sequence and the crystal structure of Drosophila spectrin, correlates well with the clinical severity of each mutation. This behavior can be approximated by the equation shown, derived by a nonlinear least squares fit to the data.
Discussion
The results presented here establish a computational approach for generating plausible models of the spectrin self-association domain and for predicting the structural consequences of point mutations involving this domain in either α- or β-spectrin. This conclusion is supported by several observations: (1) modeling theDrosophila α-spectrin 14th repeat unit accurately reflects its structure as measured by x-ray crystallography; (2) the predicted structure of the self-association domain of normal spectrin is very similar to the Drosophila structure, and valid in comparison to criteria set by other studies.17 23 This is so despite the replacement of over 70% of its residues, including 2 proline substitutions present in the human but not the Drosophilasequence, a conclusion consonant with the well-recognized conservation across broad evolutionary distances of secondary and tertiary structural features within a given protein family; and (3) the plausibility of the predicted structure itself, with polar residues on the surface, hydrophobic residues buried, an absence of steric conflicts, and a satisfactory number and variety of stabilizing noncovalent interactions.
Given the presumed validity of this model, what does it tell us about spectrin? Perhaps the most profound lesson, beyond refining by more rigorous analysis earlier concepts of the structure of the self-association domain, is that the tertiary and quaternary structure of the spectrin repeat may be precariously balanced between multiple conformational states. Several biophysical studies have noted conformational transitions in spectrin at physiologic temperatures,20 that its protease resistance is extremely sensitive to temperature and ionic strength,40 and that alternative folding states exist that might account for spectrin's unusual hydrodynamic properties.23 Yet, none of these studies would have predicted such profound sensitivity of the spectrin repeat unit and self-association unit to even seemingly minor residue substitutions.
These results also extend our understanding of the many hemolytic disorders caused by defective spectrin self-association. The majority of patients with HE and HPP have mutations in the region of α-β-spectrin self-association.7,41 Heterozygous point mutations in the α-spectrin self-association site (helix C) are among the most common mutations identified in patients with HE or HPP (Table1). Homozygous patients with such point mutations have not been described, perhaps because the complete loss of spectrin self-association may be incompatible with life. Point mutations in the β-spectrin self-association site are generally mild in the heterozygous state and severe, even fatal, in the homozygous state. Truncations that remove all or part of the COOH-terminal region of β-spectrin in the heterozygous state are associated with symptomatic elliptocytosis with poikilocytes and fragmented erythrocytes. As with homozygous α-spectrin self-association site mutants, homozygotes with truncated β-spectrin have not been observed.7 With the insights gained in this study into the forces that stabilize the self-association unit (Table 2 and Figure 3), these clinical observations can now be better understood.
As noted above, residue 28 of α-spectrin (Table 1) appears to be a “hot spot” for point mutations associated with variable clinical manifestations and is never found in the homozygous state. From molecular modeling, we see that mutations at this locus are predicted to disrupt 2 important hydrogen bonds between this residue and residues 2018 and 2022 of β-spectrin, resulting in a failure of helix C (α-spectrin) to properly dock in the β-spectrin pocket. Correspondingly, when the β-spectrin 2018 residue is mutated, as it is in spectrin Cagliari, a similar phenotype results.
An example of a mutation in the β-spectrin self-association domain that is either fatal or associated with a severe, transfusion-dependent hemolytic anemia is spectrin Buffalo, with an R→L substitution at residue β2025.42 Dynamic modeling of the spectrin Buffalo mutation predicts that hydrophobic interactions in the interior of the triple helical repeat are disrupted by the replacement of the hydrophobic uncharged leucine with a hydrophilic positively charged arginine (Figure 6; also Gallagher et al42). Another example is spectrin Providence, also fatal in the homozygous state, with a P→S substitution at residue 2019.37 This residue is adjacent to the critical hydrogen bond that stabilizes the self-association unit, noted above between α28 and β2018. Modeling demonstrates that the spectrin Providence mutation significantly disrupts the forces that stabilize the β-spectrin pocket (helices A and B) into which α-spectrin (helix C) docks (Figures 4 and 5).
In summary, these results provide important information on the putative interactions between specific amino acid residues that compose the self-association unit of human αΙβΙ-spectrin, and highlight the extraordinary sensitivity of the self-association unit to disruption by the single point mutations that are associated with clinical disorders of erythrocyte shape or stability. These data also allow a prediction of the specific residues whose disruption is likely to lead to a clinical phenotype. For example, in α-spectrin, 11 residues likely to be critical to the structure of the self-association unit have been identified by this computational approach. Mutations have been discovered in, or immediately adjacent to, 8 of these 11 residues. On this basis and on the strength of our model, we predict that clinically significant mutations involving the other 3 critical α-spectrin residues (α31, α38, and α43), or residues immediately adjacent, await discovery. A final lesson to come from this work is the clear demonstration that a complex clinical syndrome, and its severity, can be predicted essentially from first principles (ie, only with knowledge of the primary peptide sequence and a starting approximation of its structure). To our understanding, this represents perhaps the first time that such a precise correlation has been possible for these types of cytoskeletal disorders, and suggests that this approach may be valuable for predicting the consequences of mutations in other functional domains of spectrin, and potentially for other proteins as well.
Drs Scott Kennedy, Carol Cianci, and Bernard Forget are thanked for their many helpful insights and assistance with various aspects of this project.
Supported by a grant from the March of Dimes Birth Defects Foundation (to P.G.G.) and by grants from the National Institutes of Health (to P.G.G. and J.S.M.).
Portions of these results have been previously presented in abstract form at the 1999 FASEB meeting.30
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 U.S.C. section 1734.
References
Author notes
Jon S. Morrow, Department of Pathology, Yale University, 310 Cedar St, New Haven, CT 06510; e-mail:jon.morrow@yale.edu.
Supplemental data
: α-spectrin I24S mutant
: α-spectrin R28H mutant
: α-spectrin R28L mutant
: α-spectrin R28S mutant
: α-spectrin K48R mutant
: β-A2023V mutant
: β-W2024R mutant
: β-A2053P mutant
: normal spectrin
: α-spectrin I24S mutant
: α-spectrin R28H mutant
: α-spectrin R28L mutant
: α-spectrin R28S mutant
: α-spectrin K48R mutant
: β-A2023V mutant
: β-W2024R mutant
: β-A2053P mutant
: normal spectrin


This feature is available to Subscribers Only
Sign In or Create an Account Close Modal