Abstract
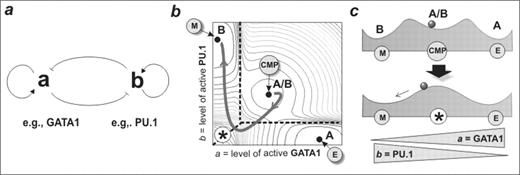
Adopting a lineage from amongst two or more options is a fundamental developmental decision in multicellular organisms. Transcription factors and their binding sites have been studied as candidate instigators of lineage. However, how the logic of gene regulatory networks translates into, for example, a binary lineage decision remains unanswered. We use mathematical modeling to understand a simple lineage decision between two hypothetical lineages A and B governed by a gene circuit containing
positive auto-regulation and
cross-inhibition between two regulatory factors, a and b (Fig. 1a).
Experimental evidence for such a circuit is provided by the regulatory interactions of GATA-1 and PU.1 in erythroid vs. myelomonocytic lineage specification. A set of non linear ordinary differential equations describing this circuit predicts a robust generic dynamics represented in a ‘potential landscape’ (Fig. 1b, and as schematic cross section, Fig. 1c). Strikingly, the model generates three stable states or ‘attractors’ which we infer to correspond to the committed A or B lineage cells and the uncommitted bipotent A/B progenitors, which are characterized by low-level co-expression of both a and b lineage-affiliated regulators. Thus, this bipotent cell fate attractor provides, for the first time, a mathematical rationale for experimental observations of co-expression of lineage-specific regulators in uncommitted cells, a phenomenon termed ‘multi-lineage priming’. The model predicts a particular trajectory in the a/b space for bipotent cells undergoing differentiation. Specifically, lineage determination involves moving towards a region in a/b space that becomes unstable (Fig. 1c bottom) so that the two lineage-committed territories in the a/b-space directly meet (asterisk, Fig. 1b). The precipitous nature of this boundary region is predicted to afford the initiation and consolidation of a lineage decision in response to relatively modest changes in cell intrinsic or extrinsic cues. We tested these predictions through examination of global gene expression profiles of uncommitted FDCP-mix cells undergoing differentiation to erythroid (E) versus myelomonocytic (M) cell fates. Consistent with the model, differentiation down these two paths follows almost identical high-dimensional ‘trajectories’ in gene expression state space during the first 24–48h towards a characteristic, destabilized state, and only hereafter do the trajectories diverge into the attractors that represent the committed cell fates. Specifically, differentiation into myelomonocytic cells was associated with the counterintuitive transient suppression of myeloid specific PU.1, precisely as predicted by the model (Fig. 1b). In conclusion, although the mathematical model describes a small network module rather than the genome-wide gene regulatory, it captures many of the essential features of a multilineage cell differentiation hierarchy and successfully predicts the genome-scale behaviour of cells undergoing differentiation and lineage specification.
Author notes
Corresponding author