Abstract
High factor VIII (FVIII) levels are known to be a risk factor for deep venous thrombosis, but the mechanisms responsible for high FVIII levels remain unclear. Here, a new phenotype “FVIII level residuum” (FVIII-R) was defined in order to eliminate the impact of common determinants on FVIII levels. We studied 13 families of patients with thrombosis and reproducibly high FVIII levels of unknown origin. Since familial clustering was evident, we looked for a possible genetic basis. A genome scan was performed with 402 evenly spaced microsatellite markers. A quantitative linkage analysis using variance component methods showed suggestive evidence for linkage of FVIII-R with a locus on chromosome 8 (logarithm of odds [LOD] = 2.1). In addition, we performed parametric exploratory linkage analysis of dichotomized FVIII-R, taking a parent-of-origin effect into account. Single-trait-locus MOD-score analysis showed suggestive evidence for linkage under an imprinting model at chromosomes 5 and 11. Furthermore, a 2-trait-locus analysis under a multiplicative model for the loci of chromosomes 5 and 11 yielded a remarkable LOD of 4.44. It confirmed the finding of paternal imprinting, obtained by single-trait-locus analysis, at both loci. Our results suggest that high FVIII levels in venous thromboembolism represent a complex trait caused by several genetic factors.
Introduction
Factor VIII (FVIII) is a key cofactor in blood coagulation. The intrinsic, FVIII-dependent pathway catalyzes conversion of factor X into factor Xa approximately 50 times more efficiently than the extrinsic pathway; it dramatically amplifies the coagulation process initiated by the extrinsic, tissue-factor–activated and factor VII–dependent pathway. The intrinsic pathway is indispensable for maintaining hemostasis, as shown by the fact that FVIII deficiency leads to hemophilia A, an occasionally severe coagulation disorder.1 Under normal conditions, FVIII levels are modulated by a variety of factors: non-0 blood groups are associated with higher FVIII levels than group 0. Most of the impact of blood type on FVIII is mediated through von Willebrand factor (VWF), the FVIII carrier molecule. Finally, FVIII levels are influenced by age and sex.2-4
Recently, high levels of FVIII, but not of VWF, were shown to be a risk factor for deep-vein thrombosis. Patients with FVIII levels higher than 1500 IU/L had an adjusted odds ratio of 4.8 (95% CI, 2.3-10.0).5 Hence, high FVIII levels represent a thrombosis risk similar to that of inhibitor deficiencies such as protein C and S deficiencies and activated protein C resistance.6 The recurrence rate is higher in thrombosis patients with high FVIII levels than in those without this coagulation abnormality.7
The mechanism by which high FVIII levels arise in thrombosis patients is unclear. These elevated levels cannot be attributed to an acute-phase reaction that often induces high FVIII activity.8 However, a familial contribution was detected in families of patients with unexplainably high FVIII levels after previous thromboembolism.9 Another study demonstrated a familial cause of high FVIII levels in families of symptomatic factor V Leiden carriers.10
So far, no molecular defects of the FVIII gene were discovered in patients with venous thromboembolism. Neither a sequence variation in the promoter and 3′ terminus nor an association between 2 highly informative CA repeats in introns 13 and 22 was found.11,12 High FVIII levels in thrombosis patients might also be due to an altered interaction of FVIII with VWF, but no clear association was shown between FVIII levels and polymorphisms in the promoter and FVIII binding region of the VWF gene.13
In order to understand the molecular background of high FVIII levels in thrombosis patients, we performed a genome scan in affected families. To our knowledge, our study represents the first genome-wide scan designed to identify loci that influence FVIII levels in families with at least one member who suffers from venous thromboembolism and who has high FVIII levels.
Patients, materials, and methods
Patients
The recruitment, sampling, methods for analyzing coagulation variables and serum proteins (eg, C-reactive protein [CRP]), and statistics have previously been published.9 Briefly, the impact of common determinants on FVIII levels was calculated based on data obtained from blood donors with normal values of prothrombin time, activated partial thromboplastin time, and inflammatory markers. Multiple regression analysis (MEDAS software; University of Würzburg) was used to define the strength of determinants, such as VWF, blood group, age, and sex, on FVIII levels. The residuals of multiple regression were used as a phenotype for linkage analysis. The new phenotype “FVIII level residuum” (FVIII-R) was calculated by the following formula: log FVIII-R = log10 (FVIII) – (0.6037 + [0.6925 × log10 {VWF}]) + (0.0336 × blood group) + (0.0009 × age/y) + (0.0048 × sex).
“Blood group” was dichotomized as “0” for 0 and “1” for non-0. “Sex” was “0” for males and “1” for females. A cutoff value of FVIII-R = 0.115 discriminates between blood donors and thrombosis patients with 90% specificity and 82% sensitivity. We selected families of thrombosis patients with reproducibly high FVIII levels of unknown origin.
Of a total of 17 families, 13 families were genotyped, with a total of 92 individuals (index patients and their relatives). Acute-phase reaction was initially an exclusion criterion, but 2 individuals showed a slightly elevated CRP (7.3 and 10.1 mg/L; cutoff value, 5 mg/L). Since CRP increase was marginal and samples were available from only one blood withdrawal, these 2 individuals were nevertheless included.
The present study was performed in accordance with the ethical standards laid down in the current version of the Declaration of Helsinki and approved by the local medical ethics committee. All subjects gave their informed consent to participate.
Genotypes
Candidate genes. We genotyped for several microsatellite markers located within or near the FVIII, VWF, and factor V genes. The microsatellite markers were identified on P1-derived artificial chromosome (PAC) clones from the human genome project containing the respective candidate genes. Accession numbers of PAC clones containing these candidate genes and microsatellite markers with primer sequences are given in Table 1. Annealing temperatures were between 55°C and 59°C. We tested for cosegregation between haplotypes and the dichotomized phenotype FVIII-R (cutoff value, 0.115). Haplotypes were assembled manually; dominant and recessive models were examined assuming complete penetrance and no phenocopies.
Microsatellite markers of candidate genes: primer sequences
Candidate gene/marker . | F . | R . |
|---|---|---|
| FVIII | ||
| DXFVIII-1 | 5′-FAM-GGAAAATGCCGCTCCATTGTTTCTAC-3′ | 5′-GGGAATAAGCCTAGAGAATGCCAAAG-3′ |
| DXFVIII-2 | 5′-TET-GGGCAAATGTACAATAGGGCAGTTTC-3′ | 5′-GGGTGACTCAGACCCTGTACTTTTACC-3′ |
| DXFVIII-3 | 5′-HEX-GGATTTTCAGGGTTCTTCGCTGCAGC-3′ | 5′-GGGCAGGTGGTATTGCCTGATTGCACC-3′ |
| FV | ||
| D1FV-1 | 5′-FAM-GTTCTGAGGGCTTAGCAAAGGTGTG-3′ | 5′-GGAAAATGAGTTGCACCACTATCCTC-3′ |
| D1FV-2 | 5′-HEX-GCTATTATTGCAGTACTGTACCCC-3′ | 5′-TCAGTCCCACAAGTCTAGGTGAGG-3′ |
| VWF | ||
| D12VWF-1 | 5′-FAM-GGGTGATGGTTTGAGTCTAATACTTC-3′ | 5′-GGGACCGCTGCCCATTGCATCAGTTAC-3′ |
| D12VWF-2 | 5′-HEX-GGTCCTGTATGTGTCAAACGTGGTCC-3′ | 5′-GGGAAAAGGGACCTCTCTCAGAGCCTC-3′ |
| D12VWF-3 | 5′-FAM-GGGCAGTGAGCCAATCCACGCCACTG-3′ | 5′-GGGTCTATCTCTGGGTGTCTATTCTAT-3′ |
| D12VWF-4 | 5′-TET-GGCAATAATGTATTCTGTGGAATCCC-3′ | 5′-GGGAACACCAGCTAACCATAGTTAAAC-3′ |
Candidate gene/marker . | F . | R . |
|---|---|---|
| FVIII | ||
| DXFVIII-1 | 5′-FAM-GGAAAATGCCGCTCCATTGTTTCTAC-3′ | 5′-GGGAATAAGCCTAGAGAATGCCAAAG-3′ |
| DXFVIII-2 | 5′-TET-GGGCAAATGTACAATAGGGCAGTTTC-3′ | 5′-GGGTGACTCAGACCCTGTACTTTTACC-3′ |
| DXFVIII-3 | 5′-HEX-GGATTTTCAGGGTTCTTCGCTGCAGC-3′ | 5′-GGGCAGGTGGTATTGCCTGATTGCACC-3′ |
| FV | ||
| D1FV-1 | 5′-FAM-GTTCTGAGGGCTTAGCAAAGGTGTG-3′ | 5′-GGAAAATGAGTTGCACCACTATCCTC-3′ |
| D1FV-2 | 5′-HEX-GCTATTATTGCAGTACTGTACCCC-3′ | 5′-TCAGTCCCACAAGTCTAGGTGAGG-3′ |
| VWF | ||
| D12VWF-1 | 5′-FAM-GGGTGATGGTTTGAGTCTAATACTTC-3′ | 5′-GGGACCGCTGCCCATTGCATCAGTTAC-3′ |
| D12VWF-2 | 5′-HEX-GGTCCTGTATGTGTCAAACGTGGTCC-3′ | 5′-GGGAAAAGGGACCTCTCTCAGAGCCTC-3′ |
| D12VWF-3 | 5′-FAM-GGGCAGTGAGCCAATCCACGCCACTG-3′ | 5′-GGGTCTATCTCTGGGTGTCTATTCTAT-3′ |
| D12VWF-4 | 5′-TET-GGCAATAATGTATTCTGTGGAATCCC-3′ | 5′-GGGAACACCAGCTAACCATAGTTAAAC-3′ |
Genome-wide linkage scan. We performed a genome-wide scan using 402 evenly spaced microsatellite markers (average heterozygosity, 0.78; minimal heterozygosity, 0.70; intermarker distances of approximately 9.5 cM according to the Marshfield genetic maps).14 DNA was prepared from blood samples using standard salt extraction–based methods. Microsatellite marker alleles were amplified with the GeneAmp polymerase chain reaction (PCR) System 9700 thermal cycler (Applied Biosystems, Foster City, CA) in a 5-μL reaction volume using the following conditions: 1x PCR buffer (50 mM KCl, 10 mM Tris [tris(hydroxymethyl)aminomethane]–HCl [pH 8.3], 2.5 mM MgCl2, 0.001% gelatin); labeled forward and unlabeled reverse primers at 250 nM and at 500 nM, respectively; 375 μM deoxynucleoside triphosphates (dNTPs); 0.2 U Taq Polymerase; and 5 ng genomic DNA. The cycling parameters were as follows: initial denaturation at 95°C for 30 seconds; 12 cycles of touchdown PCR: denaturation at 95°C for 10 seconds; annealing at between 57°C to 67°C, ΔT –0.5°C/cycle; elongation at 72°C for 30 seconds; 35 cycles: denaturation at 95°C for 10 seconds; annealing at between 51°C to 61°C for 15 seconds; elongation at 72°C for 30 seconds; and final extension at 72°C for 30 minutes. For the analysis of the marker alleles, equal amounts of the PCR products were pooled in panels containing between 4 and 10 markers. PCR products were visualized on an ABI 377 DNA Sequencer and analyzed using the Genotyper software v3.7 (Applied Biosystems).
Variance component analysis
As the first step of genome scan evaluation, a variance component analysis was carried out for the quantitative trait FVIII-R for all 23 chromosomes, by use of the program SOLAR (Southwest Foundation for Biomedical Research, San Antonio, TX).15 The multipoint approach was used for linkage analysis of the autosomes, whereas 2-point analysis was applied to the X chromosome. In the multipoint approach, a second linkage pass, conditional on the quantitative trait loci (QTL) detected in the first pass, was made. No adjustments for the FVIII-R were implemented, since this variable has already been generated by previous multiple regression analyses. However, CRP was used as a covariable due to the 2 individuals with marginally increased CRP levels. The kurtosis of the FVIII-R (–0.58) is within the normal range, so no adjustment for the logarithm of odds (LOD) scores is needed, and the standard nominal P value can be used.16
MOD score analysis
1. Single-trait locus. As a second step, parametric exploratory linkage analysis of the genome scan data was performed with the dichotomized FVIII-R. Usually, the trait model has to be specified prior to the analysis. In many cases, however, the true disease model parameters are unknown, especially in the case of genetically complex traits. Therefore, we chose a procedure called “MOD-score” analysis.17 Hence, not only information about evidence for linkage and the disease-locus position can be calculated, but also a valid, ascertainment-assumption–free method is provided to estimate the disease model parameters. We used the GENEHUNTER-MODSCORE program (Whitehead Institute for Biomedical Research, Cambridge, MA) to calculate LOD scores for a given set of predefined models, including different degrees of dominance, disease allele frequencies, and phenocopy rates. The model with a maximum LOD score is used as a starting point for fine maximization whose result is the maximum MOD score. The program GENEHUNTER-MODSCORE is a further development of GENEHUNTER-IMPRINTING (Konstantin Strauch, University of Bonn, Bonn, Germany),18 which is based on the original GENEHUNTER version 2.1.19-21 GENEHUNTER-IMPRINTING and GENEHUNTER-MODSCORE can take imprinting into account, which is also known as parent-of-origin effect. With imprinting, there are 2 heterozygote penetrances, 1 for paternal and 1 for maternal origin of the disease allele; altogether, there are 4 instead of 3 penetrance parameters.18 We performed MOD-score analysis under imprinting as well as under the nonimprinting constraint (ie, with standard 3-penetrance models). All linkage calculations with GENEHUNTER-MODSCORE are multipoint; for each chromosome, all available markers are jointly considered. Equal frequencies were used for the alleles at every marker. Since GENEHUNTER-MODSCORE is available only for an analysis of autosomal loci, the LOD-score maximization was performed manually for the X chromosome.
2. 2-trait loci. Besides increasing the evidence for linkage, testing different 2-locus disease models can show how 2 loci act, and interact, on the phenotype. Therefore, we used the program GENEHUNTER-TWOLOCUS18 to analyze pairs of genetic regions with the highest linkage peaks of the single-trait-locus analyses. Recently, GENEHUNTER-TWOLOCUS has been optimized and parallelized.22 With the new version (Konstantin Strauch and Johannes Dietter, University of Bonn, Bonn, Germany), it is now possible to analyze pedigrees with up to 18 effective meioses on a parallel computer or a workstation cluster. (Since our dataset comprises several extended pedigrees with up to 17 effective meioses, it would have taken years of computation time to analyze the dataset with the previous version.) Furthermore, the new version calculates 2-locus LOD and nonparametric linkage (NPL) scores as a function of both trait-locus positions. The results are presented by 3-dimensional plots.
A 2-trait-locus model contains the allele frequencies for each disease locus and, in addition, the matrix of 3 × 3 (in the case of imprinting of 4 × 4) penetrances. In particular, a heterogeneity, multiplicative, and an additive 2-locus disease model were applied to each pair of chromosomes.23 Considering the heterogeneity model, an at-risk genotype at either of the 2 loci can cause the phenotype on its own (“or” condition). In the context of a multiplicative model, the phenotype occurs only if an at-risk genotype is simultaneously present at both loci (“and” condition). Assuming an additive model, the penetrance of a 2-locus genotype combination is the sum of the penetrances of the single-locus effects.
The mode of inheritance (MOI) at each of the 2 putative trait loci (ie, dominant, recessive, paternal imprinting, or maternal imprinting) was adopted from the corresponding best-fitting model obtained by the single-trait-locus analysis. With these MOIs, for each of the 3 model classes, the 2-locus model was established assuming that penetrance is complete and there are no phenocopies. In addition, we also used the formulas developed by Strauch et al,24 which allow researchers to derive the penetrances of the 2-locus model from the best-fitting single-locus models, under the assumption that the model belongs to 1 of the 3 aforementioned classes (ie, heterogeneity, multiplicative, or additive model). For example, in the context of a multiplicative model, the 2-locus penetrances fij are obtained by the following formula (Strauch et al24 [Equation 14]): fij = fi · f · j/K.
Here, fi. and f.j denote the best-fitting (ie, averaged) penetrances at the first and second disease locus, respectively, and i and j stand for the respective genotypes. K is the average of the prevalences that correspond to the 2 best-fitting single-locus models. If either one of the 2-locus penetrances obtained by this equation is more than one, all penetrances need to be divided by that value. This rescaling ensures that penetrances never exceed one. The allele frequencies were adopted from the single-trait-locus analysis. For the 1 of these 6 models (ie, 3 model classes times 2 ways to determine the penetrances) that yielded the highest LOD score for a particular pair of chromosomes, we subsequently maximized the LOD score with respect to the 2-locus penetrances and the disease allele frequencies. This was done by manually restarting GENEHUNTER-TWOLOCUS for different trait models.
Results
The candidate genes encoding factor V, VWF, and FVIII were excluded by linkage tests using microsatellite markers, as a significant proportion of families did not show a cosegregation between and the dichotomized phenotype FVIII-R in any model investigated.
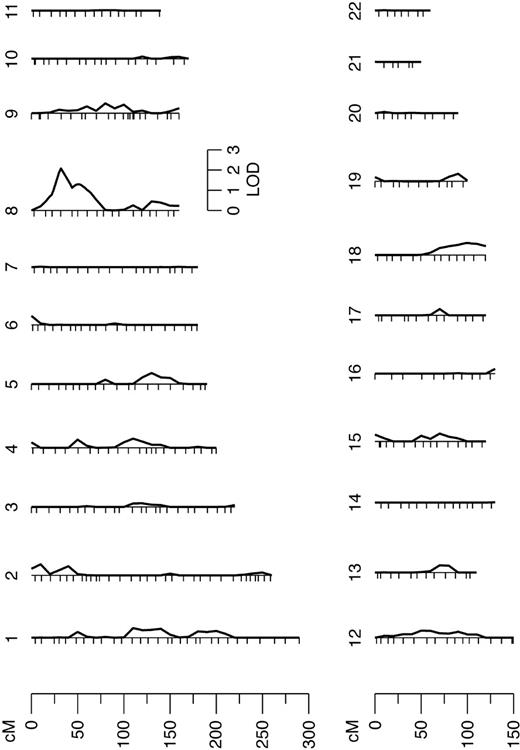
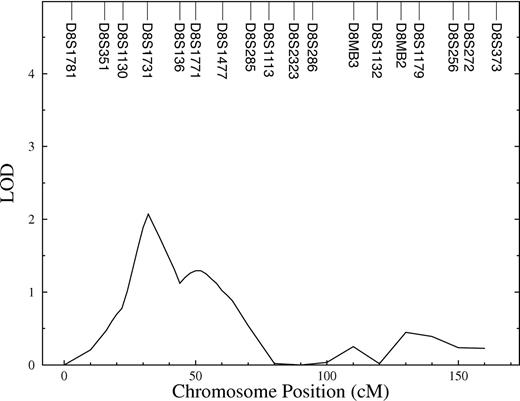
Using multipoint variance-component methods in genome scan evaluation, evidence for linkage with a QTL for FVIII-R was found on chromosome 8. The QTL had a LOD of 2.1 (P = .15). The heritability of this QTL (relative phenotypic variance that is accounted for by a QTL) was 0.67. In the initial marginal multipoint genome scan, only this region showed a LOD score higher than one (Figure 1). The interesting chromosome is shown in detail in Figure 2. In the second linkage pass, conditional on the chromosome 8 QTL detected in the first screen, evidence of linkage at other positions could not be shown. The results did not change after adjustment of FVIII-R for CRP (data not shown). For investigation of the X chromosome, a 2-point analysis was done. However, the X chromosome, where the FVIII gene is located, did not show any linkage to the quantitative trait FVIII-R.
Results from the autosomal multipoint genome scan. Hatch marks along the length of the chromosomes indicate the positions of genotyped markers.
Results from the autosomal multipoint genome scan. Hatch marks along the length of the chromosomes indicate the positions of genotyped markers.
The results for the MOD-score analysis of dichotomized FVIII-R are shown in Table 2. Assuming no imprinting, MOD scores exceeded a value of 2 for chromosome 8 (MOD = 2.02, 31 cM, D8S1731) and chromosome 9 (MOD = 2.08, 104 cM, D9S910). The locus on chromosome 8 is concordant with that obtained by the quantitative linkage analysis (33 cM). The best-fitting model obtained by MOD-score analysis was near-additive, with a disease allele frequency of .0001. For the chromosome 9 locus, the best-fitting model was near-dominant, with a disease allele frequency of .46. Assuming imprinting, the MOD for the chromosome 8 locus did not change, whereas the MOD for the chromosome 9 locus increased from 2.08 to 2.48. In addition, with imprinting, 3 additional loci with MOD scores around or more than 2 emerged on chromosome 5 (MOD = 1.98, 78 cM, D5S2003), chromosome 11 (MOD = 2.68, 92 cM, D11S4176), and chromosome 13 (MOD = 2.12, 3 cM, D13S175). Considering chromosomes 5 and 11, the paternally inherited allele hardly influences the phenotype (ie, f+/m > > fm/+, with penetrances as defined in the caption of Table 2). That means complete paternal imprinting (or maternal expression). In contrast, there is evidence for maternal imprinting in the case of the loci on chromosomes 9 and 13 (ie, f+/m < < fm/+).
Best MOD-score results for each chromosome
. | Imprinting off . | . | . | . | Imprinting on . | . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chromosome . | MOD . | Position . | P . | Penetrances . | MOD . | Position . | P . | Penetrances . | ||||||
| 1 | 0.54 | 197.97 | .02 | 0.05 0.05 0.84 | 0.91 | 173.64 | .001 | 0.05 0.05 0.32 0.32 | ||||||
| 2 | 0.87 | 228.36 | .15 | 0.03 0.03 0.30 | 1.29 | 228.36 | .005 | 0.04 0.10 0.26 0.26 | ||||||
| 3 | 1.05 | 222.83 | .01 | 0.05 0.09 0.89 | 1.13 | 94.99 | .001 | 0.05 0.39 0.05 1.00 | ||||||
| 4 | 1.30 | 40.71 | .0001 | 0.03 0.33 0.33 | 1.56 | 40.71 | .0001 | 0.03 0.12 0.40 0.40 | ||||||
| 5 | 1.10 | 161.42 | .49 | 0.00 0.00 0.66 | 1.98 | 78.31 | .03 | 0.05 0.05 0.50 0.50 | ||||||
| 6 | 1.69 | 185.83 | .0001 | 0.03 0.26 0.26 | 1.75 | 185.83 | .0001 | 0.04 0.38 0.26 0.38 | ||||||
| 7 | 0.00 | 4.1 | .001 | 0.05 0.05 0.58 | 0.33 | 178.84 | .0005 | 0.05 0.59 0.08 0.59 | ||||||
| 8 | 2.02 | 31.26 | .0001 | 0.00 0.33 1.00 | 2.02 | 31.26 | .0001 | 0.00 0.38 0.34 1.00 | ||||||
| 9 | 2.08 | 104.48 | .46 | 0.06 0.84 1.00 | 2.48 | 104.48 | .2 | 0.07 1.00 0.67 1.00 | ||||||
| 10 | 1.15 | 162.02 | .01 | 0.01 0.02 0.35 | 1.15 | 162.02 | .01 | 0.01 0.02 0.02 0.35 | ||||||
| 11 | 1.09 | 92.07 | .09 | 0.05 0.05 0.58 | 2.68 | 92.07 | .05 | 0.01 0.01 0.50 0.50 | ||||||
| 12 | 1.01 | 18.56 | .12 | 0.01 0.58 0.75 | 1.03 | 18.56 | .16 | 0.02 0.59 0.69 0.80 | ||||||
| 13 | 1.84 | 0.0 | .001 | 0.01 0.01 0.82 | 2.12 | 3.26 | .005 | 0.05 1.00 0.05 1.00 | ||||||
| 14 | 0.71 | 62.13 | .22 | 0.00 0.45 0.45 | 1.68 | 62.13 | .16 | 0.00 0.00 0.50 0.50 | ||||||
| 15 | 0.29 | 0.0 | .23 | 0.08 0.50 0.50 | 1.02 | 0.00 | .13 | 0.04 0.50 0.04 0.50 | ||||||
| 16 | 0.78 | 130.38 | .23 | 0.01 0.01 0.20 | 0.78 | 130.38 | .23 | 0.01 0.01 0.01 0.20 | ||||||
| 17 | 0.12 | 67.60 | .01 | 0.05 0.09 0.68 | 0.90 | 112.94 | .31 | 0.00 0.47 0.00 0.47 | ||||||
| 18 | 1.30 | 93.64 | .001 | 0.01 0.01 0.69 | 1.36 | 93.64 | .001 | 0.01 0.03 0.01 0.62 | ||||||
| 19 | 1.50 | 3.94 | .0001 | 0.02 0.23 0.23 | 1.71 | 3.94 | .0005 | 0.04 0.10 0.44 0.44 | ||||||
| 20 | 0.55 | 21.87 | .14 | 0.05 0.05 0.54 | 0.55 | 21.87 | .14 | 0.05 0.05 0.05 0.54 | ||||||
| 21 | 0.00 | 42.78 | .001 | 0.05 0.05 0.83 | 0.00 | 42.78 | .001 | 0.05 0.05 0.05 0.83 | ||||||
| 22 | 0.78 | 17.41 | .01 | 0.05 0.05 0.96 | 0.78 | 17.41 | .01 | 0.05 0.05 0.05 0.96 | ||||||
| X | 1.11 | 105.07 | .0013 | 0.0001 1.0 1.0 | 1.11 | 105.07 | .0013 | 0.0001 1.0 1.0 1.0 | ||||||
| 0.0001 1.0 | 0.0001 1.0 | |||||||||||||
. | Imprinting off . | . | . | . | Imprinting on . | . | . | . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chromosome . | MOD . | Position . | P . | Penetrances . | MOD . | Position . | P . | Penetrances . | ||||||
| 1 | 0.54 | 197.97 | .02 | 0.05 0.05 0.84 | 0.91 | 173.64 | .001 | 0.05 0.05 0.32 0.32 | ||||||
| 2 | 0.87 | 228.36 | .15 | 0.03 0.03 0.30 | 1.29 | 228.36 | .005 | 0.04 0.10 0.26 0.26 | ||||||
| 3 | 1.05 | 222.83 | .01 | 0.05 0.09 0.89 | 1.13 | 94.99 | .001 | 0.05 0.39 0.05 1.00 | ||||||
| 4 | 1.30 | 40.71 | .0001 | 0.03 0.33 0.33 | 1.56 | 40.71 | .0001 | 0.03 0.12 0.40 0.40 | ||||||
| 5 | 1.10 | 161.42 | .49 | 0.00 0.00 0.66 | 1.98 | 78.31 | .03 | 0.05 0.05 0.50 0.50 | ||||||
| 6 | 1.69 | 185.83 | .0001 | 0.03 0.26 0.26 | 1.75 | 185.83 | .0001 | 0.04 0.38 0.26 0.38 | ||||||
| 7 | 0.00 | 4.1 | .001 | 0.05 0.05 0.58 | 0.33 | 178.84 | .0005 | 0.05 0.59 0.08 0.59 | ||||||
| 8 | 2.02 | 31.26 | .0001 | 0.00 0.33 1.00 | 2.02 | 31.26 | .0001 | 0.00 0.38 0.34 1.00 | ||||||
| 9 | 2.08 | 104.48 | .46 | 0.06 0.84 1.00 | 2.48 | 104.48 | .2 | 0.07 1.00 0.67 1.00 | ||||||
| 10 | 1.15 | 162.02 | .01 | 0.01 0.02 0.35 | 1.15 | 162.02 | .01 | 0.01 0.02 0.02 0.35 | ||||||
| 11 | 1.09 | 92.07 | .09 | 0.05 0.05 0.58 | 2.68 | 92.07 | .05 | 0.01 0.01 0.50 0.50 | ||||||
| 12 | 1.01 | 18.56 | .12 | 0.01 0.58 0.75 | 1.03 | 18.56 | .16 | 0.02 0.59 0.69 0.80 | ||||||
| 13 | 1.84 | 0.0 | .001 | 0.01 0.01 0.82 | 2.12 | 3.26 | .005 | 0.05 1.00 0.05 1.00 | ||||||
| 14 | 0.71 | 62.13 | .22 | 0.00 0.45 0.45 | 1.68 | 62.13 | .16 | 0.00 0.00 0.50 0.50 | ||||||
| 15 | 0.29 | 0.0 | .23 | 0.08 0.50 0.50 | 1.02 | 0.00 | .13 | 0.04 0.50 0.04 0.50 | ||||||
| 16 | 0.78 | 130.38 | .23 | 0.01 0.01 0.20 | 0.78 | 130.38 | .23 | 0.01 0.01 0.01 0.20 | ||||||
| 17 | 0.12 | 67.60 | .01 | 0.05 0.09 0.68 | 0.90 | 112.94 | .31 | 0.00 0.47 0.00 0.47 | ||||||
| 18 | 1.30 | 93.64 | .001 | 0.01 0.01 0.69 | 1.36 | 93.64 | .001 | 0.01 0.03 0.01 0.62 | ||||||
| 19 | 1.50 | 3.94 | .0001 | 0.02 0.23 0.23 | 1.71 | 3.94 | .0005 | 0.04 0.10 0.44 0.44 | ||||||
| 20 | 0.55 | 21.87 | .14 | 0.05 0.05 0.54 | 0.55 | 21.87 | .14 | 0.05 0.05 0.05 0.54 | ||||||
| 21 | 0.00 | 42.78 | .001 | 0.05 0.05 0.83 | 0.00 | 42.78 | .001 | 0.05 0.05 0.05 0.83 | ||||||
| 22 | 0.78 | 17.41 | .01 | 0.05 0.05 0.96 | 0.78 | 17.41 | .01 | 0.05 0.05 0.05 0.96 | ||||||
| X | 1.11 | 105.07 | .0013 | 0.0001 1.0 1.0 | 1.11 | 105.07 | .0013 | 0.0001 1.0 1.0 1.0 | ||||||
| 0.0001 1.0 | 0.0001 1.0 | |||||||||||||
Penetrances are listed in the order f+/+, fhet, fm/m for the nonimprinting and f+/+, fm/+, f+/m, fm/m for the imprinting models (with “+” denoting the wild-type and “m,” the mutant allele), and the paternally inherited allele named first. For the X chromosome, the first penetrance line shows the parameters for females; the second line, the parameters for males (ie, f+ and fm). P denotes the disease allele frequency.
The 2-trait-locus analysis was first focused on the 2 loci for which single-locus analysis accounting for imprinting showed the highest MOD scores. This concerned chromosomes 9 and 11 whereby MOI and penetrances widely differed (Table 2). Using a heterogeneity model, analysis of chromosomes 9 and 11 showed a 2-locus LOD of 3.15. The maximum occurs at 43 cM for the chromosome 9 locus and 99 cM for the chromosome 11 locus (directly at D9S171 and D11S2000, respectively), that is, at positions different from those mentioned above (Table 3). The penetrance matrix suggests a recessive MOI at both loci. On chromosome 9, besides the MOD of 2.48 at 104 cM listed in Table 2, the single-trait-locus MOD-score analysis revealed another peak at 43 cM, with a MOD of 1.78, under a recessive model with reduced penetrance (data not shown). This second result for chromosome 9 is in accordance with the location as well as the disease model obtained by the 2-locus analysis.
Summary of the 2-trait locus results
Pair of chromosomes . | Two-locus penetrance matrix . | Disease allele frequencies, P . | Two-locus LOD score . | Position on first chromosome . | Position on second chromosome . |
|---|---|---|---|---|---|
| 9 and 11 | 0.0002 0.0002 0.0002 0.9000 | Chr 9: .0001 | 3.15 | 42.73 (directly at D9S171) | 98.51 (directly at D11S2000) |
| 0.0002 0.0002 0.0002 0.9000 | Chr 11: .0001 | ||||
| 0.0002 0.0002 0.0002 0.9000 | |||||
| 0.7000 0.7000 0.7000 0.9700 | |||||
| 5 and 11 | 0.0000 0.0000 0.1000 0.1000 | Chr 5: .03 | 4.44 | 78.31 (directly at D5S2003) | 92.07 (directly at D11S4176) |
| 0.0000 0.0000 0.1000 0.1000 | Chr 11: .05 | ||||
| 0.0000 0.0000 0.8000 0.8000 | |||||
| 0.0000 0.0000 0.8000 0.8000 |
Pair of chromosomes . | Two-locus penetrance matrix . | Disease allele frequencies, P . | Two-locus LOD score . | Position on first chromosome . | Position on second chromosome . |
|---|---|---|---|---|---|
| 9 and 11 | 0.0002 0.0002 0.0002 0.9000 | Chr 9: .0001 | 3.15 | 42.73 (directly at D9S171) | 98.51 (directly at D11S2000) |
| 0.0002 0.0002 0.0002 0.9000 | Chr 11: .0001 | ||||
| 0.0002 0.0002 0.0002 0.9000 | |||||
| 0.7000 0.7000 0.7000 0.9700 | |||||
| 5 and 11 | 0.0000 0.0000 0.1000 0.1000 | Chr 5: .03 | 4.44 | 78.31 (directly at D5S2003) | 92.07 (directly at D11S4176) |
| 0.0000 0.0000 0.1000 0.1000 | Chr 11: .05 | ||||
| 0.0000 0.0000 0.8000 0.8000 | |||||
| 0.0000 0.0000 0.8000 0.8000 |
The row of the penetrance matrix reflects the genotype at the first trait locus; the column reflects the genotype at the second trait locus, in the order f+/+, fm/+, f+/m, fm/m. Chr indicates chromosome.
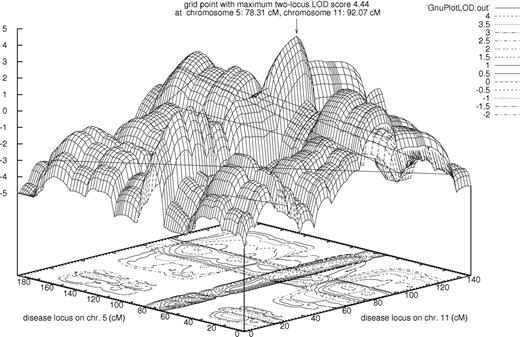
Generally, when looking at the marginal single-locus effects of a 2-locus heterogeneity model, it is likely to observe a small nonzero phenocopy rate with the averaged or best-fitting single-locus penetrances for each locus. Likewise, with a multiplicative 2-locus model, the highest penetrance of each of the 2 best-fitting single-locus models will most likely be reduced.24 Similarly to chromosome 11, the chromosome 5 with a single-locus MOD score of 1.98 (Table 2) showed reduced penetrance (0.5), so both single-locus models consistently point to a multiplicative 2-locus model. Therefore, we also performed a 2-locus analysis with these loci under a multiplicative model, and subsequently maximized the 2-locus LOD score with respect to the penetrances and disease allele frequencies. This demonstrated a remarkable LOD of 4.44 at positions 78 cM (directly at D5S2003) and 92 cM (directly at D11S4176) for the loci on chromosomes 5 and 11, respectively. These positions are identical to the ones obtained by single-locus MOD-score analysis. The 3-dimensional 2-locus LOD-score plot is shown in Figure 3. In accordance with the single-locus results, the best-fitting 2-locus model clearly favors a paternal-imprinting MOI at both disease loci (Table 3). We also performed 2-trait-locus analyses for the pair of loci on chromosomes 8 and 9, which showed the highest single-locus results without imprinting, and for the pair of loci on chromosomes 9 and 13, for which the best-fitting single-locus models with imprinting included a small phenocopy rate and complete penetrance. The 2-locus LOD scores were less than 1.5 in both cases (data not shown).
Discussion
High FVIII levels are an important risk factor for venous thromboembolism. Assuming a cutoff value that results in a 2% prevalence in the healthy population, the prevalence of unexplainably high FVIII levels in thrombosis patients varies between 11% and 18% in our patient groups. Therefore, not only an obviously increased odds ratio/relative risk but also a considerable attributable risk can be suggested. This is comparable with the factor V Leiden mutation or the prothrombin 20210G>A polymorphism, the 2 most frequent defects of inherited thrombophilia.6
Although the association of high FVIII levels and the risk for venous thromboembolism have been established consistently in the past, the pathophysiology of high FVIII levels in venous thromboembolism could not yet be unraveled. However, a dose-dependent relation between FVIII levels and the thrombotic risk suggests causality.5 As recently shown, high FVIII levels of the patients already pre-exist at the time of the thrombotic event.25 Hence, it is very likely that high FVIII levels represent a prothrombotic tendency rather than a reactive phenomenon.
It is possible that high FVIII levels exert a thrombotic risk through an associated hemostatic defect. Thus, a high FVIII activity reduces the sensitivity for activated protein (APC) in the absence of factor V Leiden.26 This acquired APC resistance was recognized as a risk factor of its own.27,28 After adjustment for APC sensitivity, however, high FVIII levels remained an independent risk factor. Recently, a genome-wide linkage screen was carried out in families who had been selected through a proband with idiopathic thrombophilia or had randomly been selected without regard to phenotype. A QTL on chromosome 18 was found to influence pleiotropic APC sensitivity and FVIII level.29
Ultimately, a familial background of high FVIII levels could be demonstrated in families with venous thromboembolism.9,10 Therefore, in the present study, we looked for a possible genetic basis of high FVIII levels in such families. For this purpose, the phenotype has to be defined very precisely. Considering the complex regulation of plasma FVIII levels is crucial for a better characterization of FVIII levels. Most factor VIII circulates as a complex with VWF, the levels of which are known to be dependent on factors such as blood group. Transiently increased FVIII levels are common in many conditions such as pregnancy or disorders such as inflammatory diseases. This highly complicates the study of the molecular basis of high FVIII levels. Therefore, patients and probands were excluded rigorously from our study if conditions and diseases could be identified that induce high FVIII levels. High FVIII levels of an index patient had to be confirmed by a second venipuncture. Finally, the FVIII-R was defined to eliminate the invariable determinants of plasma FVIII such as VWF. The effects of these determinants on FVIII level were derived from a healthy collective. This is an important aspect since the bias of additional interrelations within the families can be avoided. Therefore, we abandoned FVIII activity as phenotype and determinants such as VWF as covariables in multipoint linkage analysis.
Quantitative analysis suggests a possible QTL for FVIII-R on chromosome 8. The LOD score of 2.1 and the heritability estimate of 67% for this QTL (keeping in mind this estimator may be biased upward)30 suggest that the phenotype can largely be attributed to this QTL. The genetic signal-to-noise ratio at the detected locus is rather high. However, the pedigree size of our study is moderate, as not unusual for Germany. Thus, this may have led to the nonsignificant linkage signal with a LOD score higher than 2. The likelihood that a QTL can be localized is a function of the pedigree size and complexity.
It is a well-known fact that the power to detect linkage is reduced if the trait model specified for a parametric (LOD score) analysis is not sufficiently close to the true underlying model.17 This effect is even more pronounced in the context of multimarker analysis.31 Therefore, especially when looking at a complex trait such as FVIII levels, a MOD-score analysis, where LOD scores are maximized with respect to the disease model parameters, presents an absolutely promising route. Here, by means of MOD-score analysis of dichotomized FVIII-R, we were able to identify a linkage signal at the same locus on chromosome 8 as with quantitative analysis of FVIII-R, and at another locus on chromosome 9. When allowing for imprinting in the MOD-score analysis, further linkage signals become apparent on chromosomes 5, 11, and 13. The best-fitting models for the chromosomes 9 and 13 loci indicate maternal imprinting; for the chromosome 5 and 11 loci, paternal imprinting. Given the fact that a considerable portion of the human genome is subject to imprinting,32 this underlines the importance of adequately taking imprinting into account in the context of a linkage analysis: if imprinting is not accounted for in the analysis, an imprinted gene may simply not be found.
A MOD-score analysis represents one of the most thorough ways to analyze linkage data and minimizes the type II error. On the other hand, MOD-score analysis is clearly explorative, and so it is difficult to control the type I error. Weeks et al33 and Hodge et al34 have found, by simulation, that for MOD-scores, a critical LOD score of 3 should be adjusted by some value in the range of 0.3 to 1.0 to maintain a similar type I error, with the upper boundary being rather conservative. We put forward that loci with a MOD around 2.5, as identified in this study, show suggestive evidence for linkage. A complex trait such as high FVIII levels is most likely governed by a considerable number of genes with each having only a small effect. Therefore, in this context, we are convinced that an exploratory approach, which involves the explicit modeling of the MOI that underlies the trait, is more appropriate than a strictly inferential attitude; the number of failing genome scans in complex diseases argues in favor of this.35
Most prominently, our 2-trait-locus analysis showed a LOD of 4.44 for chromosomes 5 (at 78 cM) and 11 (at 92 cM), thereby suggesting a paternal-imprinting MOI at both putative disease loci and a multiplicative model. Here, the trait will be expressed only if an at-risk genotype is present simultaneously at both loci. The result is in accordance with the best-fitting single-trait-locus models; it clearly underlines the evidence for linkage of FVIII levels to these 2 loci.
It is even more difficult to judge the significance of 2-trait-locus LOD scores than it is to assess the significance of single-trait-locus LOD scores. If maximized over 2 recombination fractions, 2 ln(10) times the 2-locus LOD score is distributed as a ¼:½:¼ mixture of χ2 with 2 degrees of freedom (df), χ2 with 1 df, and a point mass at zero under the null hypothesis that both trait loci are unlinked to the markers.36 Under these assumptions, a single-locus LOD score of 3 corresponds to a 2-locus LOD score of 3.5. However, this correction does not reflect the maximization over disease model parameters, as we have done here in the context of our exploratory approach. Still, in order to obtain the 2-locus LOD score of 4.44, obtained with the complete sample for the chromosomes 5 and 11 loci, only a few maximization steps were performed. The 2-locus model obtained by the formulas developed by Strauch et al,24 used as the starting point for maximization, only slightly varies from the final model shown in Table 3. Therefore, the LOD of 4.44 is clearly a remarkable result. It points to 2 paternally imprinted genes, on chromosomes 5 and 11, that influence factor FVIII levels by interacting in a multiplicative fashion.
In conclusion, we have used the residual of factor VIII levels, FVIII-R, obtained by regression on its common determinants, for a genome-wide linkage analysis. A suggestive QTL on the proximal end of chromosome 8 could be shown. Moreover, modeling of imprinting substantially contributed to the genetic mapping. With MOD-score analysis of dichotomized FVIII-R allowing for imprinting, additional linkage signals appeared on chromosomes 5, 9, 11, and 13. The 2-trait-locus analysis further increases evidence of linkage. Most prominently, we found that chromosomes 5 and 11 interact in a multiplicative way such that only a combination of high-risk genotypes at both loci leads to a substantial disease risk, together with complete paternal imprinting at both the chromosomes 5 and 11 loci.
Prepublished online as Blood First Edition Paper, September 7, 2004; DOI 10.1182/blood-2004-05-2018.
Supported by grant SCHA 901/1-2, as well as by grant STR 643/1-2 (project D2 of FOR423), from the Deutsche Forschungsgemeinschaft.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 U.S.C. section 1734.
We are deeply grateful to all of the families who have participated in our study. The computation-time-intensive linkage calculations with 2-trait loci have been performed on the Sun Fire SMP Cluster of Aachen University (Aachen, Germany).

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal