Abstract
As the rates of most cancers are proportional to the fourth to fifth power of age (“log-log” behavior), it is widely believed that 5 to 6 independent mutations are necessary for malignant transformation. Conversely, the peak incidences of most cancers are similar to stem-cell mutation rates at single loci, implying only one rate-limiting mutation. Here, flow cytometrically measured red blood cells mutated at a selectively neutral locus, glycophorin A, allow observation of individual stem-cell differentiation events in a log-log malignancy, polycythemia rubra vera. Contrary to predictions from multistep models, the clone is driven by infrequent (< annual) and rare (∼ 18 per year) differentiation events. These parameters imply that malignant stem cells have a modest selective advantage. Correspondingly minor, typically less than 20%, increases in stochastic self-renewal ratios are modeled to show that single mutations can result in the observed fourth power relationship with age. The conundrum between log-log behavior and mutation rate is thereby reconcilable, with the age of onset arising not from the requirement for multiple, independent mutations but from infrequent, stochastic stem-cell division rates and single mutations causing initially minor effects, but initiating a clone whose expected number increases successively with age—an “exponential phenotype.”
Introduction
The incidences of most human cancers increase as a fourth to fifth power of age.1 Plotting logarithmically transformed data approximates to straight lines, giving rise to the term log-log cancers. As the probability of independent stochastic events occurring together in the same cell is the product of the probabilities of each event, and the corresponding rate is the first derivative with respect to time,2,3 it is widely believed there are 5 to 6 rate-limiting mutations necessary to cause cancer.4,5 However, mutation rates are many orders of magnitude too low to accommodate so many independent mutations, prompting 2- or 3-step theories.6,7 Such models postulate that the first mutation alters phenotype, either proliferative8 or mutator,9,10 to make subsequent rate-limiting mutations more likely. However, none of these models has gained general acceptance, partly because measurements on malignant stem cells are lacking.11,12
Polycythemia rubra vera (PRV) is a myeloproliferative, stem cell, clonal disorder, whose incidence increases as a fourth power of age with a peak incidence of 10.5 × 105/year at ages 75 to 80 years.13 The disease is closely associated with a point mutation, 617V>F, in the JAK2 gene,14-18 although it is currently uncertain whether the mutation is primary or secondary.19,20 In healthy individuals, about 3 × 106 hematopoietic stem cells cycle approximately annually,21 and point mutation rates are about 1 × 10−10 per cell division. The expected annual rate of production of new JAK2 617V>F mutations in stem cells is therefore 3 × 106 × 10−10 = 3 × 10−4 per individual per year or 30 per 105/year,21 similar to the peak disease incidence, implying that the disease may be due to a single such mutation. Two such independent mutations would occur together by chance over 80 years at a rate of 3 × 106 × 80 × 10−10 × 80 × 10−10 ≈ 2 × 10−10 per individual, an event unlikely to have occurred worldwide in the last century. If alternative mutations cause PRV, higher mutation rates might be applicable (eg, 10−7) per cell division for a loss of function mutation. Even then, 2 such mutations would occur together by chance at a rate of approximately 2 × 10−4 per 80 years, 1 to 2 orders of magnitude less than the peak rate of diagnoses, a calculation that does not take into account any latent period and spontaneous clone extinguishing.
However, the original mutation may effect a change in stem-cell behavior to make a second rate-limiting mutation more likely. In order to characterize this behavior, a technique for analyzing malignant stem-cell kinetics is required. Ideally, the progeny of individual stem cells would carry a marker that would be detectable in peripheral blood. Mutations at the selectively neutral blood group glycophorin A locus might provide such a marker, as red cells expressing the protein are generated by the malignant clone in polycythemia rubra vera and mutations in the highly expressed protein can be enumerated in a flow cytometer. Analysis of high “outlying” values of mutant red cells should be particularly informative. In healthy individuals, these mutant frequencies are stable22 and can be explained by both early mutations23 and mutant stem cell clones amplified by asymmetric, stochastic division21 occurring less than once per year with high numbers of sampled mutant stem cells.
Patients, materials, and methods
Detection of mutant red cells mutated at glycophorin A locus
Blood samples were obtained after permission was received from Aberdeen Royal Infirmary Ethics Committee. Approval was also obtained from the Grampian Research Ethics Committee for this study. Informed consent was obtained in accordance with the Declaration of Helsinki. Erythrocytes were analyzed as described previously.24 Staining with fluorescently labeled antibodies against M and N epitopes and subsequent flow cytometry allows enumeration of 4 mutant classes: M0, MM, N0, and NN.22 Antibodies were obtained from the International Blood Group Reference Laboratory, United Kingdom, as tissue culture supernatants, purified with protein G columns (Sigma, Poole, United Kingdom) and coupled to FITC or phycoerythrin (Sigma). Cells were counted in a Coulter Epics XL flow cytometer (Beckman Coulter, Hialeah, FL).
Clinical details
The patient with 2 glycophorin A mutant peaks presented at age 74 years with constitutional symptoms including a 12-kg weight loss. The blood count showed hemoglobin 164 g/L, hematocrit 0.64, white blood cell count 47.5 × 109/L, and platelets 1021 × 109/L. A blood count had been normal 9 years previously. Examination showed splenomegaly and hepatomegaly 10 cm and 6 cm below the costal margin, respectively. Other investigations revealed moderate renal failure with a plasma creatinine of 206 μM. A red cell mass was confirmed as being high. No BCR-ABL translocation was detected using reverse-transcription–polymerase chain reaction (RT-PCR). The JAK2 617V>F mutation was detected retrospectively, accounting for 50% to 90% of peripheral blood JAK2 representation at different time points, implying homozygosity for the mutation in the myeloid lineage. Treatment comprised venesection, aspirin, and hydroxycarbamide. Complications over the next year included episodes of gout, shingles, and thrush. Ten months after starting treatment a rash was noted, causing busulfan to be substituted for hydroxycarbamide, which was after the start of the first stem cell differentiation event. Busulfan was given intermittently for several years. The patient suffered recurrent problems with poor pulmonary function. At 4.5 years after presentation, an episode of pneumonia was complicated by acute on chronic renal failure, although dialysis was not required. The patient continued to deteriorate with progressive cachexia and ascites until death supervened.
Results
Patient survey
Ninety patients with a myeloproliferative disorder were typed serologically to ascertain MN blood group status. Forty-three were heterozygote (MN) and therefore suitable to have mutant frequencies measured. Median mutant frequencies obtained in the initial screens for the M0, MM, N0, and NN mutant classes were 6, 8, 13, and 14 per million red cells, respectively. These values were similar to healthy controls, including from other series, indicating that the mutation rate of the malignant clone was not pathologically high. As expected, if the mutant events were distributed according to random processes, and as reported previously,21 the correlations between N0 and NN and all M classes and all N are poor (r = −.03 and 0.00, respectively). There was some correlation (r = 0.32) between MM and M0 values, ascribable to difficulty in discriminating between these 2 classes of mutant cell.
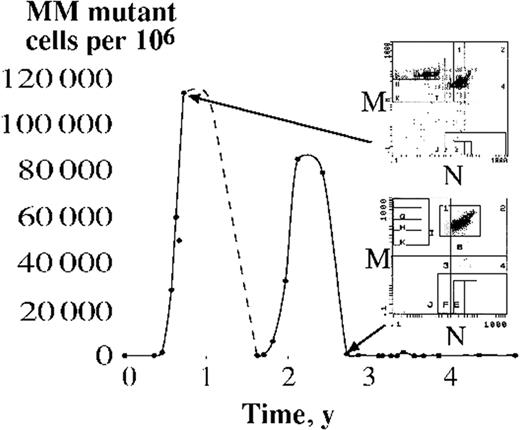
In one case, a sample taken 6 months after the initial sample showed a substantial increase in mutant frequency, and this case was sampled longitudinally for 5 years (Figure 1). The mutant frequency showed 2 peaks, each of which is interpreted as resulting from the differentiation of a malignant stem cell. After establishment of the malignant clone, a mutation at the glycophorin A locus is postulated to have occurred and resulted in at least 2 double mutant (first, oncogenic, possibly JAK2 617V>F, and second, glycophorin MN to MM) stem cells, each one differentiating to produce one of the 2 observed peaks. The peaks correspond to 4.6 × 1012 and 3.6 × 1012 red cells produced over 465 and 546 days (product of proportion of mutant red cells and red cells made per day, 2 × 1011; linear change assumed between each point), or between 1 and 2 units of blood for transfusion from each stem cell. Over 4.8 years, the proportion of 617V>F MM dual mutant red cells is then (4.6 × 1012 + 3.6 × 1012)/(4.8 × 365 × 2 × 1011) ≈ 1/42, equivalent to approximately 18 malignant stem cells contributing to erythropoiesis per year. Errors in this estimate arise from measurement, interpolation, and extrapolation. Measurement errors are relatively small as the number of mutant cells counted is so large. Uncertainties in the interpolation process are more substantial. The descent of the first event was not sampled and the use of linear interpolation between the sampled points is undoubtedly an oversimplification. In particular, the true peaks of both curves might be higher than that observed. This scenario might be estimated by extrapolating the ascents and descent to crossover. This procedure gives values of 10.1 × 1012 (or more than 2-fold higher than the linear procedure) and 4.6 × 1012 for the 2 events, which leads to an estimate of 10 malignant stem cells differentiating per year. Thus errors in interpolation might be as much as 2-fold, but are likely to result in an even smaller estimate of the number of stem cells in the malignant clone. The final source of error is extrapolation. On one hand, the different shapes of the 2 curves imply that there might be more substantial variation in the number of red cells produced from each differentiation event. On the other hand, the standard deviation of the 2 estimates using linear interpolation is a relatively low 0.68 × 1012. More observations are required to clarify these errors.
MM mutant cells measured over 5 years in a patient with polycythemia rubra vera. Each point on the graph represents the mutant frequency at the sampled time point. The dotted line indicates uncertainty, as blood was not sampled during this period. The panels on the right show examples of flow cytometric output from which the graph is based. Fluorescence from the M and N blood groups is measured on the vertical and horizontal axes, respectively. The original MN heterozygote cells are detected in box I, while MM mutant cells are detected in box G.
MM mutant cells measured over 5 years in a patient with polycythemia rubra vera. Each point on the graph represents the mutant frequency at the sampled time point. The dotted line indicates uncertainty, as blood was not sampled during this period. The panels on the right show examples of flow cytometric output from which the graph is based. Fluorescence from the M and N blood groups is measured on the vertical and horizontal axes, respectively. The original MN heterozygote cells are detected in box I, while MM mutant cells are detected in box G.
Latent period equations
Having argued that the number of rate-limiting mutations causing malignancy in stem cells is probably only one and observed that the effect of mutation(s) on the number and differentiation rates of malignant stem cells can be low, how such a single mutation might cause a fourth-power relationship of incidence with age is now explored. After an oncogenic mutation in a stem cell has taken place, it may effect 1 of 3 changes in the behavior of that stem cell and its progeny. First, it might increase the division rate. There is little experimental evidence that malignant cells divide at high rates, although such a mutation would probably increase the subsequent mutation rate during DNA replication. Second, the mutation rate might increase as a result of a “mutator phenotype.”9,10 However, the effects of both of these 2 classes of mutations seem unlikely to alter mutation rates by the several orders of magnitude required to allow a second rate-limiting mutation.12 Furthermore, neither class of mutations would result in an expanding clone.
The third change that may result is an increase in the ratio of binary fission to differentiation/apoptosis (gain-loss) rates. This change would initiate a clone whose expected size increases successively with respect to time, an “exponential phenotype.” A key feature of exponential behavior is that the change in stem-cell behavior might be initially subtle, as observed in the case reported here, but after a long enough period of time has elapsed the resultant clone size may be large. If we further postulate that clinical presentation occurs when a certain number of malignant stem cells has accumulated and include in the model the key facts that both stem-cell division and differentiation events are stochastically determined, the resultant age-specific incidence curve should be sigmoid shaped. Such a sigmoid curve might approximate to observed age-specific incidence curves when mean latent periods, which predict the time for clinical presentation rates to reach the equilibrium mutation rates, are similar to or greater than typical human life spans, approximately 80 years of age.
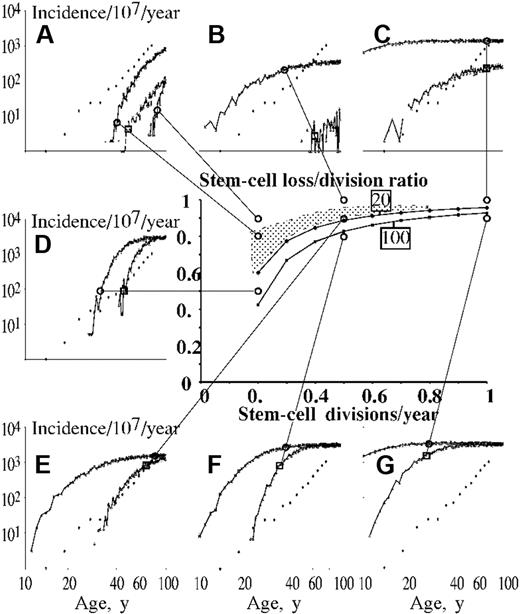
In order to help define the parameter values that would result in such latent periods, consider a simple model where μ is defined as the annual rate of differentiation and φ as the number of malignant stem cells contributing to erythropoiesis per year at clinical presentation. Then the expected value of the number of malignant stem cells at presentation, E(N), = φ/μ. Defining n as the number of cells in the clone after the initial mutation, λ as the annual probability of binary fission, and t as years after the clone was established, the expected number of stem cells in the expanding clone, E(n), = 2(1 + t(λ − μ)). At presentation n = N, thus the expected average latent period, E(t), = (logφ-log2-logμ)/(log2(λ − μ)). Solutions of this identity are shown in the central panel of Figure 2. Latent periods similar to or greater than typical human life spans are predicted when permutations of μ and λ values lie above the marked lines. It can be seen that these conditions are fulfilled when the binary fission rate is low and the rate of loss only slightly lower than the rate of division, as suggested by the observations reported here. μ and λ parameter values that fall below the marked lines give predicted age-specific incidence curves that are sigmoid but that plateau earlier than those observed.
Predicted stem-cell loss: division ratios required to confer latent periods of more than 80 years on clones initiated by mutations conferring “exponential phenotype.” Example solutions of the identity E(t) = (logφ-log2-logμ)/(log2(λ-μ)) (see “Latent period equations” under “Results” for derivation) are shown in the central graph for E(t) = 80 years. Two lines are shown, the upper corresponding to 20 malignant cells being required for diagnosis and the lower, 100 cells. A range of expected stem-cell division rates shown on the horizontal axis to a maximum of once per year with stem-cell loss (differentiation or apoptosis) rates, expressed as a proportion of expected stem-cell division rates, shown on the vertical axis. The panels surrounding the main graph illustrate predicted log-log age-specific incidence curves from a simulation program described in the main text. Each panel shows the predicted curves corresponding to the stem-cell division and loss rates indicated by the lines connecting to circles on the central graph. Predicted curves corresponding to 20 cells per year contributing to erythropoiesis are joined to the connecting line on the simulation at a circle, while those corresponding to 100 cells are joined at a square. Observed data are indicated by diamonds unconnected by lines. Combinations of stem-cell division and loss parameter values below the illustrated lines give latencies of less than 80 years, corresponding to simulations that result in flat age-specific incidence curves at ages earlier than that observed (panels F and G, both 20 and 100 cells to present; panel D, 20 cells to present). Combinations of stem- cell division and loss parameter values above the illustrated lines give latencies of more than 80 years, corresponding to simulations that result in age-specific incidence curves that mainly fail to flatten at higher ages. However, 2 other effects are also apparent. First, clones may present after chance expansion and this process results in relatively flat age-specific presentations. This effect is illustrated in panels B and C, resulting from stem-cell loss/division ratios of 1, and is particularly noticeable when numbers of stem cells required to present and stem-cell division rates are low. Indeed, in this simple model, malignant stem-cell division rates of over once per year are incompatible with exponential phenotypes causing observed log-log behavior. In addition, if stem-cell division rates are low, then high stem-cell loss/division ratios fail to cause a sufficiently high number of presenting cases (A, especially lack of simulated line corresponding to 100 cells/year contributing to erythropoiesis at loss/division ratio of 0.9). Approximate log-log behavior in this simple model for 20 malignant stem cells contributing to erythropoiesis thus results from combinations of stem-cell division and loss parameter values in the shaded area (panels A and E).
Predicted stem-cell loss: division ratios required to confer latent periods of more than 80 years on clones initiated by mutations conferring “exponential phenotype.” Example solutions of the identity E(t) = (logφ-log2-logμ)/(log2(λ-μ)) (see “Latent period equations” under “Results” for derivation) are shown in the central graph for E(t) = 80 years. Two lines are shown, the upper corresponding to 20 malignant cells being required for diagnosis and the lower, 100 cells. A range of expected stem-cell division rates shown on the horizontal axis to a maximum of once per year with stem-cell loss (differentiation or apoptosis) rates, expressed as a proportion of expected stem-cell division rates, shown on the vertical axis. The panels surrounding the main graph illustrate predicted log-log age-specific incidence curves from a simulation program described in the main text. Each panel shows the predicted curves corresponding to the stem-cell division and loss rates indicated by the lines connecting to circles on the central graph. Predicted curves corresponding to 20 cells per year contributing to erythropoiesis are joined to the connecting line on the simulation at a circle, while those corresponding to 100 cells are joined at a square. Observed data are indicated by diamonds unconnected by lines. Combinations of stem-cell division and loss parameter values below the illustrated lines give latencies of less than 80 years, corresponding to simulations that result in flat age-specific incidence curves at ages earlier than that observed (panels F and G, both 20 and 100 cells to present; panel D, 20 cells to present). Combinations of stem- cell division and loss parameter values above the illustrated lines give latencies of more than 80 years, corresponding to simulations that result in age-specific incidence curves that mainly fail to flatten at higher ages. However, 2 other effects are also apparent. First, clones may present after chance expansion and this process results in relatively flat age-specific presentations. This effect is illustrated in panels B and C, resulting from stem-cell loss/division ratios of 1, and is particularly noticeable when numbers of stem cells required to present and stem-cell division rates are low. Indeed, in this simple model, malignant stem-cell division rates of over once per year are incompatible with exponential phenotypes causing observed log-log behavior. In addition, if stem-cell division rates are low, then high stem-cell loss/division ratios fail to cause a sufficiently high number of presenting cases (A, especially lack of simulated line corresponding to 100 cells/year contributing to erythropoiesis at loss/division ratio of 0.9). Approximate log-log behavior in this simple model for 20 malignant stem cells contributing to erythropoiesis thus results from combinations of stem-cell division and loss parameter values in the shaded area (panels A and E).
However, this scenario does not incorporate features such as clones being extinguished or expanding to reach diagnostic levels by chance. To investigate the predicted effects of such mutations in more detail a simulation program was written.
Modeling age-specific incidence
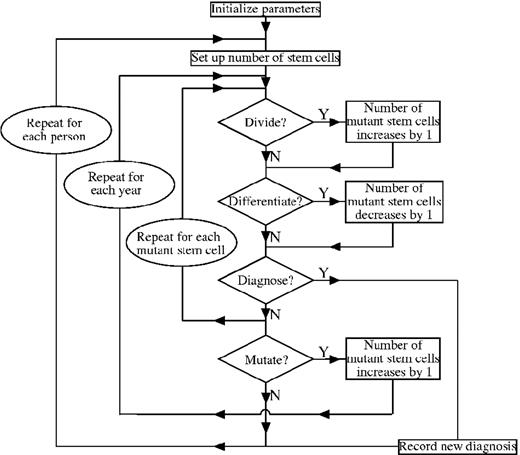
The initial model is outlined in Figure 3, with the code itself given in Document S1 (available on the Blood website; see the Supplemental Materials link at the top of the online article). Myeloproliferative clones are initiated by single mutations occurring in one of 3 × 106 stem cells at a constant rate, 10−9, per cell division. Neither the mutation rate nor the number of stem cells affects the shape of the predicted age-specific incidence curves, although they do affect the absolute values (simulations not shown). Clonogenic mutations decrease the loss-gain ratio. Both differentiation/apoptosis and division are stochastically determined.25,26 Diagnosis occurs if the number of malignant stem cells reaches the number of malignant stem cells contributing to erythropoiesis per year/μ. Simulations were run for cohorts of 107 individuals over 99 years.
Organization of program modeling new mutations and fate of subsequent clones. The program is outlined in the text and listed in Document S1.
Organization of program modeling new mutations and fate of subsequent clones. The program is outlined in the text and listed in Document S1.
There are too many parameters and insufficient observations on stem-cell behavior to estimate all parameter values accurately. Instead, the properties of this simple model are explored to illustrate the implications of the 3 important parameter values (stem-cell binary fission rate, differentiation/apoptosis rate, and number of stem cells needed to present) for age-specific incidences. As expected, simulations give rise to sigmoid age-specific incidence curves (Figure 2). It was first confirmed that μ and λ parameter pairs that fall below the lines predicted by identity 1 predict sigmoid age-specific incidence curves that plateau too early (Figure 2D,F,G).
However, not all parameter pairs above the line result in appropriate curves due to 2 effects. First, diagnoses may occur after random expansions of clones, an effect that does not increase markedly with time and is significant when low numbers of cells to present are required and loss-gain ratios are close to unity (Figure 2B,C). Second, increasing the loss-gain ratios shifts the sigmoid curves to the right but also increases the proportion of clones that extinguish by chance or never attain a critical size. These effects are manifest as a lowering of the plateau level so that few diagnoses are noted when μ is low and λ is close to 1 (Figure 4A). Thus, for any given number of malignant stem cells to present, μ and λ parameter pairs that result in approximately appropriate curves are given by permutations that lie immediately above the curves given by identity 1 (illustrated by the shaded area for 20 cells to present in Figure 2).
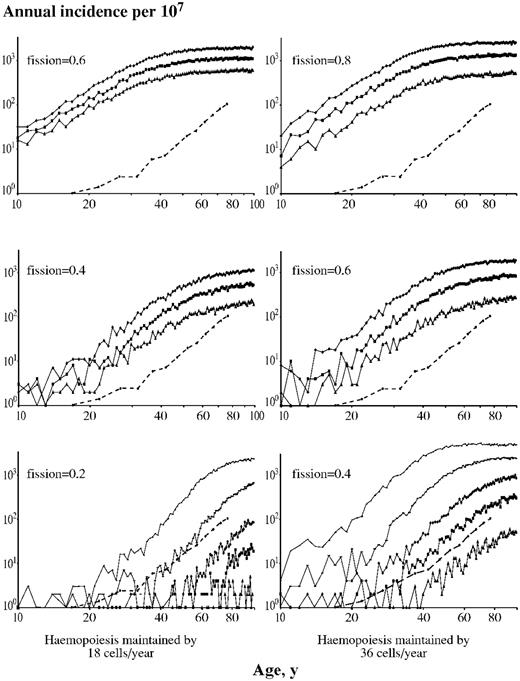
Illustrative simulations showing age-specific incidence curves predicted from single mutation conferring an “exponential phenotype.” Each point on the graph is the predicted annual rate of new clinical presentations, marked on the vertical axes, at each age, marked on the horizontal axes. The model was run on 107 individuals using a mutation rate of 10−9 per cell division. Circles joined by interrupted lines are observed data. The lowest predicted line on each graph, marked by triangles, results from the malignant stem cells having expected division/differentiation–apoptosis ratios of 1 (ie, no selective advantage), with successively higher curves resulting from ratios of 0.95, 0.9, 0.8, and 0.6 (indicated by ■, ◆, —, and -, respectively). The left-hand triad of panels is based on hematopoiesis being maintained by 18 stem-cell differentiation events per year and the right hand triad, 36 such events. The expected stem-cell binary fission rates per year used in the simulations are indicated on each graph.
Illustrative simulations showing age-specific incidence curves predicted from single mutation conferring an “exponential phenotype.” Each point on the graph is the predicted annual rate of new clinical presentations, marked on the vertical axes, at each age, marked on the horizontal axes. The model was run on 107 individuals using a mutation rate of 10−9 per cell division. Circles joined by interrupted lines are observed data. The lowest predicted line on each graph, marked by triangles, results from the malignant stem cells having expected division/differentiation–apoptosis ratios of 1 (ie, no selective advantage), with successively higher curves resulting from ratios of 0.95, 0.9, 0.8, and 0.6 (indicated by ■, ◆, —, and -, respectively). The left-hand triad of panels is based on hematopoiesis being maintained by 18 stem-cell differentiation events per year and the right hand triad, 36 such events. The expected stem-cell binary fission rates per year used in the simulations are indicated on each graph.
Having demonstrated the basic features of predictions of a single mutation causing an exponential phenotype, the model was refined to reflect current understanding of hematopoiesis more fully. In particular, the model used in Figure 2 assumes that an adult complement of stem cells is established instantaneously at birth. More plausibly, the adult complement of stem cells was held constant after the age of 20 years, but taken to be proportional to body mass before this time. Mutant cells arising before attainment of the adult complement are allowed to expand at expected rates greater than that after attainment of the adult complement, in accordance with expansion of the stem-cell pool. Earlier mutations are thus rarer, although they result in disproportionately larger clone sizes,23 as first described by Luria and Delbrück,27 thereby demonstrating the quantized nature of mutations.
Including these features alters the predicted gradients of log-log age-specific incidence curves in a way that approximates better than the simple model to observed data. Figure 4 illustrates predictions from varying the values of the number of malignant stem cells contributing to erythropoiesis per year (18 and 36 shown here), binary fission rates (0.2-0.8 per year shown here), and differentiation-apoptosis rates (60%-100% of fission rate shown here). For 18 stem-cell differentiation events per year and fission rates of 0.4 or more per year, the upper plateau of the sigmoid curve is clearly seen at ages younger than 80 years for all loss rates, even to 100% fission rates (Figure 3 left panels). Fission rates less than 0.4 per year result in the plateau not being seen at younger than 80 years, except at loss-gain ratios less than 0.7. Postulating higher numbers of cells to present (Figure 3 right panels) allows a higher range of fission rates to result in log-log behavior. It is striking that the gradient of the ascending part of the sigmoid curve, plotted logarithmically, seen with most of the parameter values explored here is approximately 4, although higher gradients can be seen with higher numbers of cells to present and low loss-gain ratios (simulations not shown). Thus log-log behavior with a gradient of approximately 4 results from rare, infrequently dividing malignant stem cells as implied by the parameters of the case reported here, although there are insufficient observations for the values of each of these parameters to be estimated accurately.
The stochastic nature of stem-cell division and differentiation or apoptosis is critical to this hypothesis. If true, this behavior also implies most clones acquiring a selective advantage extinguish spontaneously as noted in other models.28 For the phenotype suggested here, the proportion extinguishing ≈ loss/gain (simulations not shown). Thus for the range of ratios suggested by the data in this paper, 60% to 99% of clones gaining exponential mutations will not survive, which would explain why peak malignancy rates are often 1 to 2 orders of magnitude less frequent than single gene mutation rates per organ. Two other recently reported observations on myeloproliferative disease are also explainable with the model. First, the phenomenon of 0.25% to 10% of circulating leukocytes carrying the JAK2 617V>F mutation being detectable in 1% of patients without a myeloproliferative disease20 as stem cells carrying the mutation differentiate and are thereby lost to the stem cell pool. Second, the variance of clone size sampled over many years is considerable29 as a low number of mutant cells are sampled.
Discussion
If the observations presented in Figure 1 are explained by the differentiation of single malignant stem cells, such cells are more infrequent and slowly dividing than previously believed. Together with the known stochasticity of division and differentiation of stem cells, these parameters exacerbate the known problems of accommodating multihit models of carcinogenesis. Instead, the parameters suggest that log-log behavior may result from a single mutation that modestly increases the stem-cell division/differentiation–apoptosis ratio. This “exponential phenotype” replaces the conventional explanation for log-log behavior from the need for several rate-limiting mutations to a new paradigm explained by a single mutation interacting with infrequent, stochastically determined stem-cell division, which would reconcile the long-standing conundrum between mutation rate and rate-limiting mutation number. Although myeloproliferative disorders are unusually benign malignancies, that this model might apply to other log-log cancers is suggested by the low mutation rate and infrequency of stem cells in other tissues. Two other epidemiologic observations also provide support for the generality of this model. First, most log-log tumors display a marked flattening in incidence over the age of 75 years.30,31 This property follows naturally from the model proposed here, whereas multihit models predict a continuing increase. Second, cancers caused by exposure to short-term chemotherapy or radiotherapy are characterized by a unimodal peak incidence rather than a progressive increase as would be predicted by several rate-limiting steps.32,33
Several criticisms of the reasoning outlined here should be highlighted. Most importantly, the demonstration that a model with several variable parameters is able to predict observed age-specific incidences does not prove that this model is true. Furthermore, several assumptions used in construction of the model may not be true. The most critical assumptions in this regard are probably that the observed peaks in glycophorin mutant cells are due to individual stem-cell differentiation events, that these events originate from the malignant clone, that single mutations are able to increase stem-cell fission rate to differentiation/apoptosis rate ratios and that clinical presentation is determined mainly by attaining a threshold number of clonal stem cells. Judging the plausibility of these assumptions is necessarily subjective.
While other malignancies have been described that have constant age-specific onsets consistent with single hits,34 such examples are rare and are believed to result from mutations that arise in lineage-committed cells, causing blocks to differentiation that present after only short latent periods. By contrast, the “exponential phenotype” postulated here has an initially subtle effect on stem-cell behavior and is probably difficult for a stem cell to counteract using other regulatory mechanisms, illustrated by how common selection of one X-chromosome over the other is in females.35 Such mutations may be relatively common, in which case a high proportion of stem cells in elderly individuals would have inherited one of them. However, only the subset of such mutations that have similar effects in more differentiated cells, so generating sufficient malignant cells to present clinically, would cause malignancy.
The main argument against log-log cancers being caused by a single rate-limiting mutation is that numerous mutations have been documented in human malignancies,36-38 and several mutations appear necessary for the full expression of a malignant phenotype.4 These discrepancies might be resolved by a single underlying rate-limiting mutation causing a clone large enough to provide further mutations at non–rate-limiting rates.38 Clearly, more observations on human malignant stem cells are required, although the observations in this paper imply that malignant stem cells are even more infrequent than those measured by most current techniques39,40 as their expected rate of division is similar to murine life spans.
An Inside Blood analysis of this article appears at the front of this issue.
The online version of this article contains a data supplement.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734.
Acknowledgments
This work was funded by Aberdeen Royal Infirmary Leukemia Research Fund.
I thank Joan Rae for help with sample collection, Sarah Canning for sample processing, and David Wilson and Prof Stanislaw Urbaniak for access to the flow cytometer.
Authorship
Contribution: M.A.V. designed and performed research, analyzed data, and wrote the paper.
Conflict-of-interest disclosure: The author declares no competing financial interests.
Correspondence: Mark A. Vickers, Department of Medicine and Therapeutics, Aberdeen University Medical School, Polwarth Building, Foresterhill, Aberdeen AB25 2ZD, United Kingdom; e-mail: m.a.vickers@abdn.ac.uk.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal