Key Points
Hindered diffusion becomes the dominant force of molecular movement in a thrombus.
The thrombus core acts as a selective molecular prison.
Abstract
Hemostatic thrombi formed after a penetrating injury have a heterogeneous architecture in which a core of highly activated, densely packed platelets is covered by a shell of less-activated, loosely packed platelets. In the first manuscript in this series, we show that regional differences in intrathrombus protein transport rates emerge early in the hemostatic response and are preserved as the thrombus develops. Here, we use a theoretical approach to investigate this process and its impact on agonist distribution. The results suggest that hindered diffusion, rather than convection, is the dominant mechanism responsible for molecular movement within the thrombus. The analysis also suggests that the thrombus core, as compared with the shell, provides an environment for retaining soluble agonists such as thrombin, affecting the extent of platelet activation by establishing agonist-specific concentration gradients radiating from the site of injury. This analysis accounts for the observed weaker activation and relative instability of platelets in the shell and predicts that a failure to form a tightly packed thrombus core will limit thrombin accumulation, a prediction tested by analysis of data from mice with a defect in clot retraction.
Introduction
Platelets are central to hemostasis, helping to form a hemostatic plug or thrombus without occluding the vessel. Recent work has shown that hemostatic thrombi formed following penetrating laser or probe injury in the cremaster muscle microcirculation are heterogeneous with respect to important properties such as the extent of platelet activation, platelet packing density, porosity, and the distribution of thrombin activity.1,2 This heterogeneity is organized into a structure in which a core of highly activated platelets close to the injury site is covered by a shell of loosely adherent and less activated platelets.1 In the first manuscript in this series,3 we showed that the transport of plasma proteins in the gaps between platelets is also heterogeneous, being slower in the core than in the shell. These findings raise new questions about the origins of the thrombus architecture that we and others have observed.
Computational methods are useful for answering questions about complex systems, complementing experimental approaches and generating new hypotheses. Computational approaches have been used to model the hemostatic process (reviewed in Wang and King4 ), but few have explicitly examined the impact of platelet packing density or molecular transport through the hemostatic plug.5-8 Here, we propose that considering molecular transport leads to a more comprehensive understanding of how the internal organization of a hemostatic plug develops. Drawing on published studies4 and observations from the first manuscript of this series,3 we have examined plasma velocity in a hemostatic plug modeled in 2 dimensions. To simulate solute transport, we have modeled hemostatic thrombi as a porous media comprised of regions with distinct physical characteristics that represent the core and shell. Using this computational framework, we have reproduced experimental data and then explored the role of the core by comparing solute transport through a simulated hemostatic thrombus with or without a core.
The results show that once platelet accumulation begins, plasma velocity slows by orders of magnitude and relatively few platelets are needed to create a sheltered environment where diffusion, rather than convection, is dominant. Our results further emphasize that the core and shell are distinct physical microenvironments and that the thrombus core acts as a selective molecular prison retaining some soluble agonists to increase their effective concentration. Predictions made based on this model are tested in the third manuscript of this series.9
Methods
Model setup
We used 2 models to study intrathrombus transport. The first model, which was only used to study the flow characteristics inside the thrombus, is a 2-dimensional (2D) representation of a thrombus with platelets represented explicitly by ellipses and will be referred to as the “explicit-platelet” model in the text. For this model, we used computational fluid dynamics based on the Stokes equation to resolve the flow in the narrow gaps between platelets as well as in the lumen surrounding the thrombus (Figures 1-3). In the second model, the thrombus is represented as a 2-compartment homogeneous porous medium. For this model, which includes species transport, we adopted a mathematical description similar to Kim et al.7 Here, we applied the Stokes equation for the lumen region and a Brinkman equation for the thrombus. These equations are coupled with convection-reaction diffusion equations to study solute transport in the thrombus (Figures 4-7). Both models were implemented and solved using COMSOL, version 4.3a.
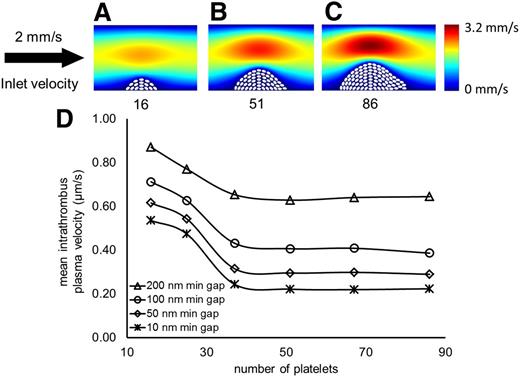
Thrombus size does not determine intrathrombus plasma velocity. (A-C) Successive stages of thrombus growth with corresponding number of platelets and bulk plasma velocity field. (D) The horizontal axis represents the number of platelets in the hemostatic thrombus. The vertical axis shows the average plasma velocity computed between the platelets. In all cases, the inlet vessel velocity is modeled as a pressure-driven parabolic profile with a maximum velocity of 2 mm/second (s).
Thrombus size does not determine intrathrombus plasma velocity. (A-C) Successive stages of thrombus growth with corresponding number of platelets and bulk plasma velocity field. (D) The horizontal axis represents the number of platelets in the hemostatic thrombus. The vertical axis shows the average plasma velocity computed between the platelets. In all cases, the inlet vessel velocity is modeled as a pressure-driven parabolic profile with a maximum velocity of 2 mm/second (s).
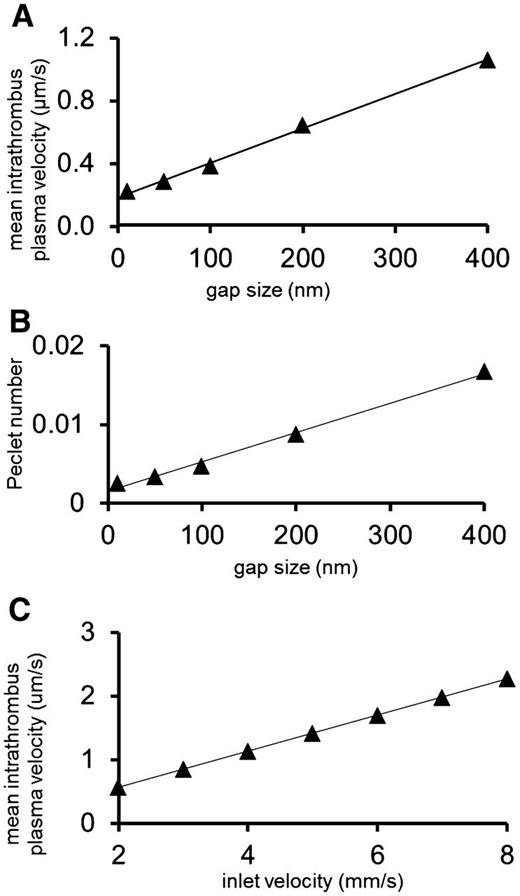
Platelet gaps, plasma velocity, and porosity in a hemostatic plug. (A) The relationship of minimum gap size to mean intrathrombus plasma velocity. (B) The relationship between minimum gap size and the Peclet number shows that intrathrombus transport is dominated by diffusion. (C) The average velocity in a hemostatic thrombus increases linearly with the inlet velocity (slope = 0.28), but even when the velocity is quadrupled the velocity between platelets is still in the μm/s range.
Platelet gaps, plasma velocity, and porosity in a hemostatic plug. (A) The relationship of minimum gap size to mean intrathrombus plasma velocity. (B) The relationship between minimum gap size and the Peclet number shows that intrathrombus transport is dominated by diffusion. (C) The average velocity in a hemostatic thrombus increases linearly with the inlet velocity (slope = 0.28), but even when the velocity is quadrupled the velocity between platelets is still in the μm/s range.
Heterogeneous gap size distribution. Based on experimental data (A-B), 2 different architectures were designed with a subset (the core) of more tightly packed platelets at the front (C) or in the center (D) of the hemostatic plug. The smallest gaps are 200 and 10 nm between white and gray platelets, respectively. In all cases, the inlet vessel velocity is modeled like a pressure-driven parabolic profile with a maximum velocity of 2 mm/s. (E) Sample regions in a prethrombus area, behind core platelets (gray) and shell platelets (white) with their respective computed velocity magnitudes. (F) Average intrathrombus plasma velocity computed for geometries with the core in the front (black) or middle (red). Platelet packing density, but not the core location, determines the average velocity between platelets.
Heterogeneous gap size distribution. Based on experimental data (A-B), 2 different architectures were designed with a subset (the core) of more tightly packed platelets at the front (C) or in the center (D) of the hemostatic plug. The smallest gaps are 200 and 10 nm between white and gray platelets, respectively. In all cases, the inlet vessel velocity is modeled like a pressure-driven parabolic profile with a maximum velocity of 2 mm/s. (E) Sample regions in a prethrombus area, behind core platelets (gray) and shell platelets (white) with their respective computed velocity magnitudes. (F) Average intrathrombus plasma velocity computed for geometries with the core in the front (black) or middle (red). Platelet packing density, but not the core location, determines the average velocity between platelets.
Solute transport can be computationally reproduced. The diagram of the geometry used to simulate the solute transport process is shown above each graph. The hemostatic plug is designed as a combination of 2 homogeneous regions, denoted as “core” and “shell,” in which physical characteristics such as packing density and fibrin content are defined by porosity, permeability, and effective diffusivity. The graphs show data (Welsh at al3 ) and simulations of caged fluorescent albumin transport. The vertical axis shows the normalized concentration of fluorescent albumin from experimental data and simulations. Solute transport is faster in the shell than in the core in vivo. These phenomena can be computationally reproduced only by assuming that the core and shell have different packing densities (A) and not otherwise (B).
Solute transport can be computationally reproduced. The diagram of the geometry used to simulate the solute transport process is shown above each graph. The hemostatic plug is designed as a combination of 2 homogeneous regions, denoted as “core” and “shell,” in which physical characteristics such as packing density and fibrin content are defined by porosity, permeability, and effective diffusivity. The graphs show data (Welsh at al3 ) and simulations of caged fluorescent albumin transport. The vertical axis shows the normalized concentration of fluorescent albumin from experimental data and simulations. Solute transport is faster in the shell than in the core in vivo. These phenomena can be computationally reproduced only by assuming that the core and shell have different packing densities (A) and not otherwise (B).
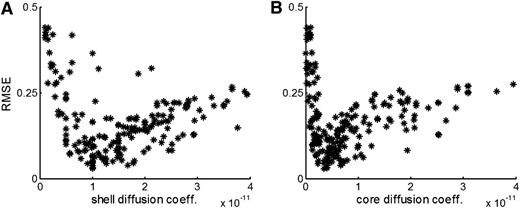
Global sensitivity analysis. We implemented global sensitivity analysis performing 200 simulations, each with a different combination of parameters, and evaluated the fit (RMSE value) to the experimental data describing the transport of caged fluorescent albumin. We plot the values sampled for the effective diffusion coefficient in the shell (A) and in the core (B) with the corresponding RMSE value. The effective diffusion coefficient values show a robust signal with respect to the fit, independently of the choice of the other parameter values. From this, we estimate the effective diffusion coefficient to be 1 × 10−11 and 4 × 10−12 m2/s for shell and core, respectively.
Global sensitivity analysis. We implemented global sensitivity analysis performing 200 simulations, each with a different combination of parameters, and evaluated the fit (RMSE value) to the experimental data describing the transport of caged fluorescent albumin. We plot the values sampled for the effective diffusion coefficient in the shell (A) and in the core (B) with the corresponding RMSE value. The effective diffusion coefficient values show a robust signal with respect to the fit, independently of the choice of the other parameter values. From this, we estimate the effective diffusion coefficient to be 1 × 10−11 and 4 × 10−12 m2/s for shell and core, respectively.
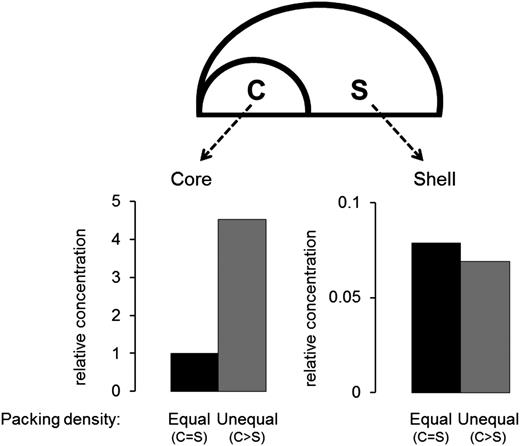
The core is retentive. Relative concentrations in a simulated core and shell were calculated when a substance with the same diffusion coefficient as albumin was released from a 1-µm patch under the core. Simulations were run until steady state was reached, comparing 2 scenarios in which the packing density in the core was either equal to or greater than the shell. Calculated concentrations were normalized to the value attained in the core when the packing densities are equal. The graph on the lower left shows steady-state concentrations in the core, which are higher when density in the core is greater than the shell. The graph on the lower right shows steady-state concentrations in the shell, which are lower than in the core and unaffected by having core density greater than the shell.
The core is retentive. Relative concentrations in a simulated core and shell were calculated when a substance with the same diffusion coefficient as albumin was released from a 1-µm patch under the core. Simulations were run until steady state was reached, comparing 2 scenarios in which the packing density in the core was either equal to or greater than the shell. Calculated concentrations were normalized to the value attained in the core when the packing densities are equal. The graph on the lower left shows steady-state concentrations in the core, which are higher when density in the core is greater than the shell. The graph on the lower right shows steady-state concentrations in the shell, which are lower than in the core and unaffected by having core density greater than the shell.
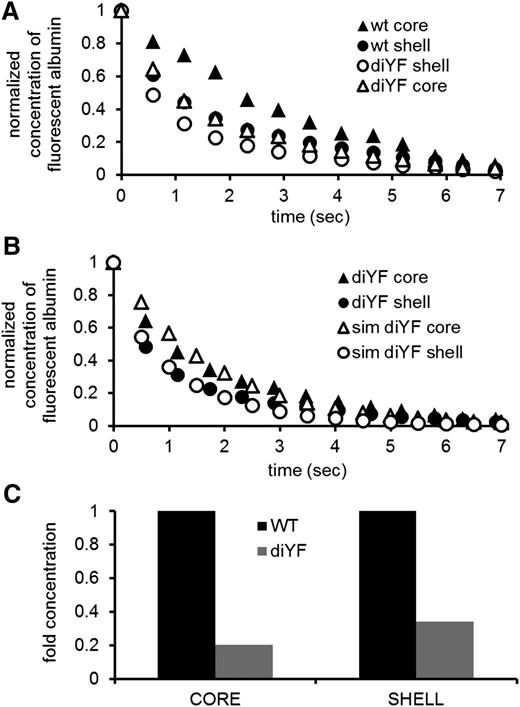
Larger gaps predict faster solute transport and decreased platelet activation. (A) Solute transport, as measured by caged fluorescent albumin, is faster, both in the core (circles) and in the shell (triangles), of diYF mice (empty symbols) compared to wild-type (wt) mice (filled symbols) (experimental data are from Stalker et al,9 Figure 2). (B) Simulations (empty symbols) predict measured solute transport data, for both the core (circles) and the shell (triangles) of diYF (filled symbols) mice. (C) Simulation of solute release from a wall region under the core predicts that the average concentration at steady state will be lower in both regions in the diYF mice.
Larger gaps predict faster solute transport and decreased platelet activation. (A) Solute transport, as measured by caged fluorescent albumin, is faster, both in the core (circles) and in the shell (triangles), of diYF mice (empty symbols) compared to wild-type (wt) mice (filled symbols) (experimental data are from Stalker et al,9 Figure 2). (B) Simulations (empty symbols) predict measured solute transport data, for both the core (circles) and the shell (triangles) of diYF (filled symbols) mice. (C) Simulation of solute release from a wall region under the core predicts that the average concentration at steady state will be lower in both regions in the diYF mice.
Thrombus design for the explicit-platelet model
We designed a thrombus with size and geometry based upon in vivo images of stable thrombi (supplemental Figure 1, available on the Blood Web site). Each platelet was modeled as an ellipse with minor and major semiaxes of 0.6 µm and 1 µm. To investigate packing density, we changed the dimensions of the ellipses without modifying their positions. We modeled the internal core-and-shell thrombus architecture by selectively changing the dimensions of a subset of platelets. Additional details may be found in the supplemental Materials.
Solute transport
We used the “species transport in porous media package” in COMSOL, version 4.3a, solving the convection-reaction-diffusion equation:  , where c is the concentration of chemical species of interest, D is the diffusion coefficient, u is the velocity vector field, and R describes sources of the various chemical species. We imposed an initial uniform concentration of a tracer solute in the vessel, 0 solute concentration at the influx boundary, and then ran the simulation until the concentration inside the thrombus regions decreased to 0. Additional details may be found in the supplemental Materials.
, where c is the concentration of chemical species of interest, D is the diffusion coefficient, u is the velocity vector field, and R describes sources of the various chemical species. We imposed an initial uniform concentration of a tracer solute in the vessel, 0 solute concentration at the influx boundary, and then ran the simulation until the concentration inside the thrombus regions decreased to 0. Additional details may be found in the supplemental Materials.
Single parameter sensitivity analysis
The value of each of the 6 parameters (porosity, permeability, and effective diffusion coefficient for the core and shell regions of the thrombus) was varied by 50% above and below its base case regressed value. For each variation, the transport simulation was run, and the error between the simulation and experimental data evaluated. The sensitivity score with respect to each of the 6 parameters was calculated as the average of the root mean square error (RMSE) of the 2 simulations (+50% and −50%) relative to the RMSE of the base case fit.
Global sensitivity analysis
Each parameter was chosen randomly from a uniform distribution (Table 1). Each combination was chosen using a Latin hypercube sampling design. We simulated transport through the hemostatic thrombus and computed the RMSE between the simulation and the experimental data. We repeated this process 200 times with every simulation resulting from a different combination of parameters.
| Parameter . | Minimum . | Reference . | Maximum . | Reference . |
|---|---|---|---|---|
| Porosity − ε | >0 | Minimum physically possible | 1 | Maximum physically possible |
| Permeability (m2) − κ | 10−18 | 14 | 10−14 | 14 |
| Effective diffusion coefficient (m2/s) − D | 10−13 | Current paper | 5 × 10−11 | 11 |
| Parameter . | Minimum . | Reference . | Maximum . | Reference . |
|---|---|---|---|---|
| Porosity − ε | >0 | Minimum physically possible | 1 | Maximum physically possible |
| Permeability (m2) − κ | 10−18 | 14 | 10−14 | 14 |
| Effective diffusion coefficient (m2/s) − D | 10−13 | Current paper | 5 × 10−11 | 11 |
Results
We began by examining the impact of thrombus size and packing density on plasma velocity within a hemostatic thrombus, the former by varying the number of platelets and the latter by varying the size of the gaps between platelets. To replicate results from the mouse injury model, we considered a vessel 30 μm in diameter and designed growing platelet masses in which the smallest gaps were located in either the middle or the front of the mass. These manipulations were meant to reproduce a hemostatic thrombus growing (an increase in platelet number), consolidating (a reduction in gap size), or developing the characteristic core-and-shell architecture (heterogeneous gap distribution). Unless otherwise stated, all of the simulations had an inlet centerline velocity of 2 mm/s, typical of what is measured in similar size vessels under physiological conditions.
The results show that once a threshold is reached, the average plasma velocity within a hemostatic thrombus is minimally affected by the number of platelets within the thrombus. With as little as 16 platelets, the average intrathrombus plasma velocity was ∼3 orders of magnitude less than the bulk velocity (Figure 1A). Further increases in platelet number had only a minimal effect (Figure 1B-D). Using the largest thrombus geometry shown in Figure 1C, we examined how gap size and distribution affect molecular movement in a thrombus. The range of gap sizes that we considered was selected from electron microscopy studies in the literature.10 We found that even when the minimum gap is as much as 400 nm, the average velocity within the thrombus is <2 µm/s (Figure 2A). As gap size decreased, so did velocity, highlighting the ability of platelets to hinder flow.
Convection vs diffusion
The relative impact of convection and diffusion is shown in Figure 2B, where minimum gap size is plotted against the Peclet number (see “Methods”), a value that estimates the relative contributions of convection and diffusion. A Peclet number of 1 indicates that convection and diffusion contribute equally, whereas a value ≪1 indicates that diffusion dominates over convection. The results show that the small pore sizes within the thrombus produce a microenvironment in which molecular transport is dominated by diffusion. This effect was not substantially affected by bulk plasma velocity. For instance, even with a fourfold increase in lumen velocity, from 2 to 8 mm/s, the intrathrombus velocity was still within the µm/s range (Figure 2C).
The impact of heterogeneous thrombus architecture
The presence of a tightly packed thrombus core1 was simulated by decreasing the minimum gap size between a subset of platelets from 200 to 10 nm (Figure 3 gray ellipses). The simulated core region was placed either in the front (Figure 3A,C) or in the center (Figure 3B,D) of the platelet mass to determine whether the location of the core affected plasma velocity within the mass. Figure 3E illustrates how the plasma velocity is affected by the presence of platelets. The velocity of the plasma near the vessel wall immediately upstream of the thrombus is ∼0.5 mm/s. Between platelets, this falls to 1 µm/sec, decreasing even further where the narrowest gap between platelets is 10 nm. Notably, the location of the core had little effect (Figure 3F).
Solute transport within the hemostatic plug
In the first manuscript in this series,3 we provide experimental evidence that solute transport rates are slower in the core than in the shell. Solute transport measures how molecules move in the complex geometry of a hemostatic plug. Particle movement in the absence of obstacles and convection is described by Brownian motion (ie, the diffusion coefficient). The diffusion coefficient of albumin11 is 6 × 10−11 m2/s, which given similarity in mass, resembles that of thrombin12 (8 × 10−11 m2/s) but is much lower than nonprotein agonists such as adenosine 5′-diphosphate (ADP)13 (50 × 10−11 m2/s). We next asked whether the observed differences in transport can be reproduced assuming that the core and shell are characterized by microenvironments with different transport properties, as opposed to being just 2 distinct geographical regions.
To do this, we designed a thrombus with size, shape, and architecture based on the in vivo observations. Because the model that we used to study flow characteristics places large computational demands when trying to resolve flow features in the narrow gaps between individual platelets, we modeled the thrombus as 2 homogeneous regions with physical characteristics described by 3 parameters: porosity, permeability, and the effective diffusion coefficient (Figure 4A). Porosity represents the fraction of empty space in the mass, with larger gaps corresponding to larger porosity values. Permeability is the ability of a porous material to allow fluid to pass through, thus describing pore connectivity. The effective diffusion coefficient represents how a molecule of a certain size diffuses through a porous material. The presence of solid boundaries within a porous media hinders molecular movement, and as a result the effective diffusion coefficient is smaller than the free diffusion coefficient. Note that these material characteristics are independent. Thus, it is possible for 2 materials, or 2 hemostatic plug regions, to have the same porosity but different permeability or diffusion coefficients and vice versa.
Porosity values for the core and shell were obtained in vivo.1 Permeability values were obtained in vitro14 and do not distinguish between core and shell regions. These experimental estimates served as an initial guide for our simulations. We assumed the existence of a core and a shell, and in both regions assigned a value for each of the 3 parameters. Thus, each simulation is specified by 6 parameters, and the value of a parameter for the core cannot be larger than the value of the corresponding parameter for the shell. We simulated the transport through the hemostatic plug, computed the average concentration in each region over time, and compared it to the experimental data (see “Methods”). We found a set of parameters for which there is a good agreement between the simulation and experimental data (Figure 4A). Thus, by hypothesizing that the core is more densely packed than the shell, we found a combination of parameters (Table 2) that reproduces the experimental data. Assuming instead that the core is as densely packed as the shell does not lead to a good agreement between experimental data and simulations (Figure 4B).
Parameter values used in Figure 4A
| Parameter . | Core . | Shell . |
|---|---|---|
| Porosity − ε | 0.2 | 0.4 |
| Permeability (m2) − κ | 10−17 | 10−16 |
| Effective diffusion coefficient (m2/s) − D | 4 × 10−12 | 10−11 |
| Parameter . | Core . | Shell . |
|---|---|---|
| Porosity − ε | 0.2 | 0.4 |
| Permeability (m2) − κ | 10−17 | 10−16 |
| Effective diffusion coefficient (m2/s) − D | 4 × 10−12 | 10−11 |
Due to the multidimensional nature of the parameter space, it is possible for multiple combinations of parameters to fit the data equally well. Because it is not feasible to investigate all possible combinations, we used sensitivity analysis to determine the impact of each parameter on solute transport. Two complementary approaches were used: single-parameter and global sensitivity analysis. Single parameter analysis reveals how sensitive the simulation output is to the change of a single parameter. The model is sensitive to the effective diffusion coefficient and, to a lesser degree, porosity (Table 3). Conversely, the model is insensitive to the choice of the permeability value. The large sensitivity to the effective diffusion coefficient fits well with the results obtained in the previous section where we observed that the intrathrombus microenvironment is diffusion dominated. The global sensitivity analysis was performed by running simulations using different parameter combinations. We found a nonlinear trend with a well-defined minimum for the effective diffusion coefficient (Figures 5A-B). This shows that choosing the correct value for the effective diffusion coefficient results in a good fit to the data regardless of other parameter values. This confirms the results of the single-parameter sensitivity analysis. Moreover, the minimum in the scatter plots represents a theoretical estimate of the effective diffusion coefficient values in a hemostatic plug (compare the minima in Figure 5 with the values shown in the bottom row of Table 2). In contrast, the same analysis applied to porosity and permeability shows no pattern (supplemental Figure 5), confirming our previous conclusion that molecular movement in the thrombus is dominated by diffusion.
Release of soluble agonists from the injury site
Potent platelets agonists, such as thrombin, are primarily produced in proximity of the injury site.1,2 We examined how a closely packed core region affects the distribution of thrombin-like solutes that are produced in a small region under the core of the hemostatic plug. Parameter values estimated in the previous section (porosity, permeability, and effective diffusion coefficient) were used to describe the physical characteristics of the core and the shell. We simulated the constant release of a substance with the same diffusion coefficient as albumin from a 1-μm patch on the vessel wall under the core. We ran the simulation until it reached steady state (usually at ∼30 s) and computed the average concentrations of the solute in the simulated core and shell, comparing a model in which packing density is greater in the core than the shell (which is what we observe in vivo) with a model in which packing densities are equal in the core and shell.
The results are summarized in Figure 6 with the computed concentrations normalized to the value calculated in the core when the packing densities are equal. Having a densely packed core increases the effective concentration of soluble agonists in the core ∼4.5-fold (Figure 6, lower left). In contrast, the concentration attained in the shell was 10- to 20-fold lower than in the core, regardless of whether the core and shell were consider as having equal or unequal packing density (Figure 6, lower right). The core is thus acting as a selective molecular prison, where molecules may get “trapped” in a gap size-dependent manner. Conceivably, as platelets transition to a state of full activation and fibrin polymerization fills the available spaces within the core,1 the core becomes a prison for an even broader set of molecules.
Testing model predictions
The simulations described so far show that packing density dictates transport rates. We hypothesized that a decrease in packing density would modify the thrombus architecture by reducing the size of the core and total platelet accumulation. This would happen because: (1) larger average gaps between platelets decrease the effective concentration of agonists, especially in the core, which is where we have shown1,2 that most of the thrombin is found; (2) the decrease in agonist concentration reduces platelet activation, leading to a smaller core; and (3) fewer fully activated platelets diminish the paracrine effects of agonists such as ADP and TxA2 released from activated platelets, causing a decrease in total platelet accumulation.
We tested this hypothesis using data obtained with mice carrying a substitution of phenylalanine for 2 tyrosine residues (diYF) in the cytoplasmic domain of the β subunit of the αIIbβ3 integrin. The diYF substitution impairs integrin outside-in signaling and slows clot retraction in vitro.15 In the accompanying manuscript,9 we show that this mutation also impairs retraction in vivo, suggesting that hemostatic thrombi in these mice will have larger gaps between platelets compared with wild-type. Figure 7A shows the comparison of caged fluorescent albumin transport experiments in control and diYF mice (Stalker et al9 ; Figure 2). Consistent with our hypothesis, transport in both the core and the shell is faster in the diYF mice.
We modeled conditions in the diYF mice using the parameter values listed in Table 2, changing only the value of the effective diffusion coefficient in both the core and the shell to simulate the looser platelet packing. We used the RMSE to estimate the fit to the data. We found a good agreement with the experimental data (Figure 7B) when the value of the effective diffusion coefficient was doubled in both the core and shell (Dc = 8x10−12 m2/s; Ds = 2x10−11 m2/s). These results illustrate that we can reproduce the experimental observations of solute transport in diYF mice by modeling a thrombus with decreased packing density compared with wild-type.
Next, we used the parameter set that provided the best fit to the diYF data to simulate the constant release of an agonist from the vessel wall and compared the results with the wild-type simulation (Figure 7C). This simulation demonstrates that when the gaps between platelets become larger, as in the diYF mice, the concentration of thrombin-like agonists is decreased in the core and the shell. This supports our hypothesis that a reduction in the size of the core in diYF mice is due not to the inability of platelets to be activated or to a decrease in agonist production but to an increase in the size of the gaps between the platelets.
Discussion
The hemostatic response requires platelets to adhere to the vessel wall and then to each other, forming part of a plug that prevents further bleeding and fostering the local production of thrombin and fibrin. Here, we have considered platelets from a different perspective, focusing on their ability to alter their local environment by obstructing the free flow of plasma-borne molecules into the region of injury and the free flow of platelet-derived molecules out of the region. Our goal was to understand how the physical attributes of a platelet-enriched thrombus impact the hemostatic response, an idea previously examined by Kim et al7 using data obtained in vitro. To accomplish this goal, we used experimental solute transport data3 to inform numerical simulations.
The results show that by acting as obstacles, platelets can retard plasma flow by orders of magnitude. Our estimates for intrathrombus velocity are in agreement with in vitro estimates14 and 3-dimensional (3D) simulations.4 A further reduction in plasma velocity is achieved by decreasing the size of the gaps between platelets. The end result is the formation of a sheltered microenvironment where diffusion, rather than convection, becomes the dominant mechanism for molecular movement. Using simulations benchmarked on experimental evidence, we estimate the effective diffusion coefficient for an albumin-like substance to be 5 times smaller in the shell than in the vessel lumen and even smaller in the core. We expect the effective diffusion coefficient of thrombin to be even smaller given its binding kinetics.
Solute transport within a hemostatic mass has recently received attention. Hindered protein transport through a fibrin cap has been considered,7 with results suggesting that the cap limits thrombus growth. Hindered transport was also considered as a mechanism capable of stopping thrombus growth.6,16 In a previous study from our group, transport through a reconstructed 3D thrombus was examined.4 The results show that a protein-sized solute released from the bottom of the thrombus will escape from the sides. Thus, a variety of experimental and theoretical approaches have reached similar conclusions. This speaks to the generality of hindered transport as a mechanism to limit thrombus growth following injury in order to achieve hemostasis while avoiding unnecessary vascular occlusion. Hemostasis begins with platelets being recruited at a site of injury, stably attached platelets becoming progressively more activated by potent agonists, such as thrombin, which are produced primarily at the site of injury.1,2 As platelets become more activated, the gaps between them shrink, and soluble agonists can either be trapped (ie, thrombin) or prevented from penetrating in quantities sufficient to drive excessive platelet activation and fibrin deposition (ie, prothrombin and other coagulation factors).16,17
As in any model, certain simplifications and assumptions are necessary. In the explicit-platelet model (Figures 1-3), where only fluid flow was examined, platelets were assumed to be ellipsoids with semi-axes of 1 and 0.6 µm. However, our results suggest that intrathrombus flow is governed primarily by gap size and not by the details of platelet shape. Platelet shape change, variability in platelet size, or the presence of larger cells such as leukocytes would all alter the flow, but we assume that such effects are implicitly captured by varying the gap size distribution. The effect of gap size distribution on flow is illustrated in Figure 1. Intrathrombus velocity is progressively decreased as the gap size decreases. For all gap size distributions considered, the flow is always in the regime of low Reynolds, Peclet, and Womersley numbers (supplemental Materials). Under the physiological conditions we examined, we can expect constant laminar flow in the lumen and diffusion to be dominant in the thrombus.
The homogeneous species transport model, which is based on a porous medium representation of the thrombus, is parameterized using measurements obtained in vivo.3,9 The parameters in the homogeneous transport model (diffusivity, permeability, and porosity) implicitly capture the macroscopic details such as platelet packing density or shape change and fibrin content, or any combination of the two. Our species transport simulations (Figures 4-7) depend, therefore, on an effective diffusivity derived from experimental data.
The solute transport data (Figure 4) show the loss of fluorescence over time in a 2D thin slice (∼0.5 µm) of the thrombus taken with a confocal microscope. The caged fluorescent albumin, however, elutes from the thrombus in a 3D volume; thus, it can take paths that cannot be accounted for in a 2D model. Macroscopically, 2D simulations assume that transport in the third dimension is not important or that the thrombus is “long” in the neglected dimension. Although this is obviously a simplification, the 2D results remain meaningful for analyzing the effects studied here. In the supplemental Materials, we show that in a 3D diffusion-only version of the thrombus where the depth-to-length aspect ratio approaches 0.5, the 2D simulation results become a good approximation to the 3D simulations (supplemental Figure 7B).
An increasing amount of in vivo evidence is consistent with the model we propose. Porosity measurements indicate that the differences between core and shell are size selective.1 Thrombin activity can be detected only in the core.1,2 Full platelet activation, as measured by P-selectin expression, occurs only in the core, whose size is neither decreased by eliminating ADP signaling nor enhanced by boosting it.1 Artificially increasing the plasma prothrombin concentration does not increase total platelet accumulation in an arterial injury model,18 suggesting that increasing the concentration of thrombin precursor does not lead to increased thrombin production or increased platelet recruitment. Finally, our model predicts that changing the dynamics of transport changes the effective concentration of agonists and thus thrombus architecture. We verified this prediction experimentally in an in vivo mouse model characterized by a defect in platelet retraction. We found that thrombi with larger gaps developed smaller cores and accumulated less fibrin.9
Taken together, this study and the accompanying manuscripts demonstrate the importance that gap size has in shaping molecular transport and platelet activation status. Although others have addressed the potential importance of gaps19 or estimated gap sizes,7,20,21 this is the first effort of which we are aware that combines observational and computational approaches to understand the effect of gap size on thrombus growth. In 3D, one can expect that some platelets, or portions of platelets, may be in direct membrane-membrane contact (0 nm) or in indirect contact mediated by protein-protein interactions (tens of nm), integrin-fibrinogen-integrin interactions (<100 nm),22 or the binding of von Willebrand factor to the glycoprotein Ib/IX/V complex (possibly ≥100 nm).23 In this microstructure, it is important to know the gap size distribution, because that is what ultimately determines transport rates.
In conclusion, the results presented here demonstrate that the interactions between platelet biology and molecular transport are important in shaping thrombus architecture and determining platelet activation status. These interactions have already been partially unmasked by in vivo data,1 indicating that the outer, less closely packed region of a hemostatic thrombus is primarily driven by platelet-derived, highly diffusible molecules such as ADP and is therefore most susceptible to P2Y12 purinergic receptor antagonists. In contrast, the tightly packed core region is primarily driven by the less diffusible thrombin and is more susceptible to thrombin inhibitors. The effects of intrathrombus transport should therefore be considered when designing new and improved antiplatelet agents.
The online version of this article contains a data supplement.
There is an Inside Blood Commentary on this article in this issue.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734.
Acknowledgments
This work was supported by the National Institutes of Health, National Heart, Lung, and Blood Institute (P01HL40387 to L.F.B., R01HL119070 to T.J.S. and L.F.B., and R01HL103419 to S.L.D. and L.F.B.), and the American Heart Association (11SDG5720011 to T.J.S.). J.D.W. and M.T. were supported by a National Institutes of Health training grant T32-HL07439.
Authorship
Contribution: M.T. designed and conducted the computational studies, analyzed data, and wrote the manuscript; J.D.W. and T.J.S. conducted experiments and analyzed data; T.S. and S.L.D. analyzed and interpreted data; and L.F.B. analyzed data and wrote the manuscript.
Conflict-of-interest disclosure: The authors declare no competing financial interests.
Correspondence: Lawrence F. Brass, University of Pennsylvania, Perelman School of Medicine, 815 BRB II/III, 421 Curie Blvd, Philadelphia, PA 19104; e-mail: brass@mail.med.upenn.edu.



This feature is available to Subscribers Only
Sign In or Create an Account Close Modal