Key Points
Free VWF in flow extends gradually as shear stress increases and not abruptly with the presumed globule-stretch transition.
Polymer simulations suggest that VWF behaves as an uncollapsed, random chain with minimal monomer-monomer interactions.
Abstract
von Willebrand factor (VWF) is a multimeric blood protein that acts as a mechanical probe, responding to changes in flow to initiate platelet plug formation. Previously, our laboratory tests had shown that using single-molecule imaging that shear stress can extend surface-tethered VWF, but paradoxically, we found that the required shear stress was higher than reported for free-in-flow VWF, an observation inconsistent with basic physical principles. To resolve this inconsistency critical to VWF’s molecular mechanism, we measured free-VWF extension in shear flow using pulsed laser stroboscopic imaging of single molecules. Here, laser pulses of different durations are used to capture multiple images of the same molecule within each frame, enabling accurate length measurements in the presence of motion blur. At high shear stresses, we observed a mean shift in VWF extension of <200 nm, much shorter than the multiple-micron extensions previously reported with no evidence for the predicted sharp globule-stretch conformational transition. Modeling VWF with a Brownian dynamics simulation, our results were consistent with VWF behaving as an uncollapsed polymer rather than the theorized compact ball. The muted response of free VWF to high shear rates implies that the tension experienced by free VWF in physiological shear flow is lower than indicated by previous reports and that tethering to platelets or the vessel wall is required to mechanically activate VWF adhesive function for primary hemostasis.
Introduction
von Willebrand factor (VWF) is a multimeric glycoprotein that circulates in blood and helps regulate hemostasis.1,2 Consisting of 40 to 250 monomeric units arranged end to end, each VWF concatemer can have a contour length up to 15 μm.3-5 Hydrodynamic forces regulate VWF’s molecular mechanisms via tension-dependent binding. Binding partners include GPIbα for platelet recruitment,6-10 collagen for immobilization of damaged blood vessels,11,12 other VWF molecules for amplifying activation,13-15 and ADAMTS13 protease for VWF size regulation.15-19 VWF activation is premised upon its sensitivity to force, with conformational changes expected above a critical shear threshold. Extension is thought to expose binding sites, but sufficient tension is also required to allosterically activate binding to recruit platelets and initiate hemostasis.
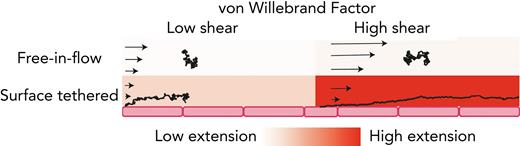
Recently, Fu et al6 tethered VWF to a surface and measured VWF response to shear flow at the single-molecule level, monitoring extension and ability to bind the platelet protein GP1bα. Surface-tethered VWF (Figure 1A, red) showed shear-dependent increases in extension up to the maximum shear stress applied (1280 dyn/cm2). For reference, normal arterial shear stress is between 10 and 70 dyn/cm2 but is estimated to reach >400 dyn/cm2 in injured arterioles.20
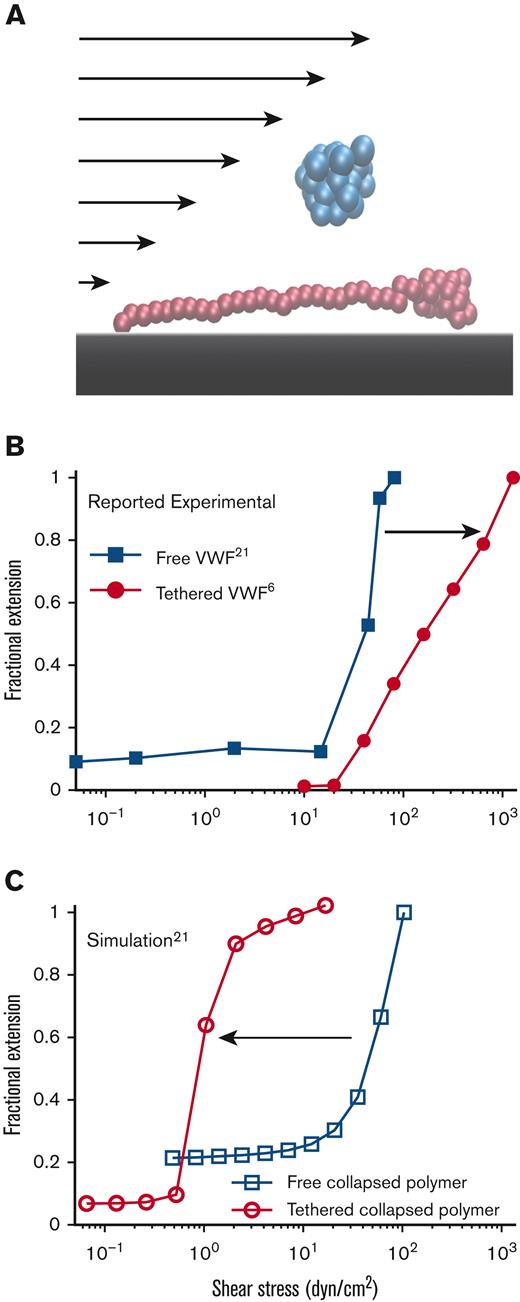
Free vs surface-tethered VWF extension under flowshows inconsistent behavior. (A) Diagram illustrating21 free-in-flow (blue) vs surface-tethered (red) VWF with applied shear flow. (B) Data from the study by Schneider et al22 (blue) showing normalized extension vs shear stress for free VWF and data from the study by Fu et al6 (red) showing normalized extension vs shear for tethered VWF. Required shear stress for free-VWF extension is expected to be higher than required shear stress for surface-tethered extension, but experimentally, the opposite was observed. (C) Predictions of mean extension in response to shear stress based on a Brownian dynamics model with a strong Lennard-Jones (LJ) interaction potential proposed by Schneider et al22 for both a free-in-flow (blue) and tethered (red) polymer. Lengths are normalized based on the maximum observed length in the direction of flow.
Free vs surface-tethered VWF extension under flowshows inconsistent behavior. (A) Diagram illustrating21 free-in-flow (blue) vs surface-tethered (red) VWF with applied shear flow. (B) Data from the study by Schneider et al22 (blue) showing normalized extension vs shear stress for free VWF and data from the study by Fu et al6 (red) showing normalized extension vs shear for tethered VWF. Required shear stress for free-VWF extension is expected to be higher than required shear stress for surface-tethered extension, but experimentally, the opposite was observed. (C) Predictions of mean extension in response to shear stress based on a Brownian dynamics model with a strong Lennard-Jones (LJ) interaction potential proposed by Schneider et al22 for both a free-in-flow (blue) and tethered (red) polymer. Lengths are normalized based on the maximum observed length in the direction of flow.
In an earlier study,22 free VWF in pure shear flow was directly imaged. There appeared to be an extension of free VWF from a collapsed ball to an elongated filament ∼15 μm in length, with abrupt extension at ∼50 dyn/cm2. Vascular injury was proposed to increase shear stress above this critical threshold, causing free-in-flow VWF to extend and adhere to the vessel wall at injury sites. A coarse-grained polymer model calibrated to match the extending behavior was used to model VWF.22,23 The basic model of a collapsed polymer has been subsequently updated to simulate VWF behavior on a surface,24–26 in elongational flow,27,28 in shear flow,29-31 and size regulation through enzymatic cleavage.17,32,33
These tethered and free VWF single-molecule experiments present a paradox: the putative shear stress required to extend free VWF was lower than the shear stress required to extend surface-tethered VWF (Figure 1B). Simulations (Figure 1C), based on the model by Schneider et al,22 were applied to both free and surface-tethered scenarios. They predict that surface-tethered VWF should extend at shear stresses 100× lower than free VWF. Independent of simulations, basic physical arguments predict a lower shear stress to extend tethered vs free polymers.30,34,35
To resolve this discrepancy, we experimentally investigated the response of free VWF in shear flow using a new method to properly account for motion blur. In addition, we updated the coarse-grained polymer model to match our new results and previously published single-molecule experiments. We found that an uncollapsed polymer is sufficient to describe mesoscopic VWF behavior in flow, which complements a recent study that found evidence for a random coil description of VWF.36 By contrast, models representing VWF as a collapsed polymer are difficult to reconcile with single-molecule data.
Our results indicate that single molecules of free VWF in physiological shear flow experience much lower internal tension than previous experiments and models predicted. This has major consequences for understanding the molecular mechanisms of hemostasis initiation, including the tension-dependent activation of VWF binding in flow and VWF size regulation and further clinical significance for von Willebrand disease, thrombotic thrombocytopenic purpura, and Heyde syndrome.4
Methods
VWF and control preparation
Recombinant, therapeutic grade VWF was size-fractionated to select for longer multimers and labeled with Alexa 488 N-hydroxysuccinimide ester as described in the study by Fu et al.6 For the positive control, M13mp18RF DNA was labeled with YOYO-1. Fluorescent beads (diameter = 0.11 μm determined by the manufacturer) were used for the negative control. Imaging buffer was 60% (w/w) sucrose with 20 mM N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (pH 7.4), 150 mM sodium chloride, 0.02% Tween-20, and 0.5 mg/ml bovine serum albumin.
PULSIS
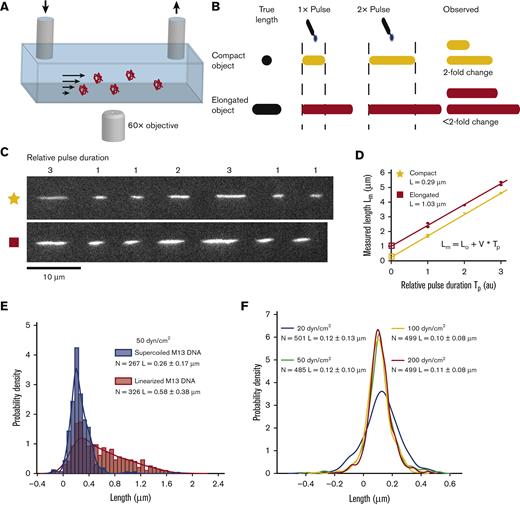
Molecules were imaged with a lab built total internal reflection fluorescence microscope (60× oil immersion objective). A pressure-driven flow system was used to flow VWF through microfluidic channels (Figure 2A). To correct for motion blur, we developed pulsed laser stroboscopic imaging of single molecules (PULSIS) (Figure 2B-D), which images each molecule multiple times with different duration laser pulses. This enabled us to build a relationship between the laser pulse duration and the observed streak length on a per-molecule basis which was used to determine a “zero-pulse” or motion blur–corrected length. Molecules were imaged with pulsed laser illumination, which followed a pattern of 1-on, 3-off, 1-on, 3-off, 2-on, 3-off, 3-on, and 3-off with the frequency of the pulse pattern tuned to the fluid velocity (supplemental Methods, section 1, available on the Blood website).
PULSIS. (A) Basic schematic of the pressure-driven flow system and imaging setup, not to scale. (B) Cartoon depiction of PULSIS. Objects are imaged with different duration pulses and by comparing the relative lengths, we can accurately measure the lengths of moving objects and distinguish point objects from elongated objects. (C) Example experimental PULSIS trajectories of fluorescently labeled linearized DNA at 50 dyn/cm2. (D) Example relationship between measured length of pulse Lm (μm) vs relative pulse duration Tp (arbitrary time units) for the 2 DNA PULSIS trajectories in panel C. For each trajectory, streak lengths are measured and a linear regression performed of the form Lm = L0 + V × Tp, with fitting errors according to York et al.37Lm is the illuminated streak length that we measure, and Tp is the relative pulse duration defined by the pulse pattern (1, 2, or 3). The linear fit gives us the particle velocity V, and the y-intercept L0 represents the length of the molecule observed with an infinitesimally short pulse, that is, with no motion blur. The first trajectory (yellow) has a corrected length of 0.29 μm and resembles a compact object. The second trajectory has a corrected length of 1.03 μm and represents an elongated object. Error bars on pulse length are based on goodness of fit to predicted pulse shape (supplemental Methods). (E) Positive control showing histogram of PULSIS-determined lengths of double stranded M13 DNA plasmid both in supercoiled (blue) and linearized (red) state at 50 dyn/cm2, imaged in sucrose buffer. Histograms are of motion blur–corrected lengths of hundreds of single molecules. The examples (trajectories and analysis) from Figure 2C and D are 2 statistics from the linearized (red) distribution. Histograms are displayed along with kernel density estimates. Kernel density estimation is a method for smoothing histograms by applying a Gaussian kernel to each point.38 A Gaussian kernel was used with bandwidth set by the Silverman rule.39 (F) Negative control showing kernel density estimate for PULSIS motion blur–corrected beads at different shear stress (manufacture determined diameter of 0.11 μm). Raw histograms are shown in supplemental Figure 1. Number of measurements and mean length and standard deviation for each condition are shown in panels E and F.
PULSIS. (A) Basic schematic of the pressure-driven flow system and imaging setup, not to scale. (B) Cartoon depiction of PULSIS. Objects are imaged with different duration pulses and by comparing the relative lengths, we can accurately measure the lengths of moving objects and distinguish point objects from elongated objects. (C) Example experimental PULSIS trajectories of fluorescently labeled linearized DNA at 50 dyn/cm2. (D) Example relationship between measured length of pulse Lm (μm) vs relative pulse duration Tp (arbitrary time units) for the 2 DNA PULSIS trajectories in panel C. For each trajectory, streak lengths are measured and a linear regression performed of the form Lm = L0 + V × Tp, with fitting errors according to York et al.37Lm is the illuminated streak length that we measure, and Tp is the relative pulse duration defined by the pulse pattern (1, 2, or 3). The linear fit gives us the particle velocity V, and the y-intercept L0 represents the length of the molecule observed with an infinitesimally short pulse, that is, with no motion blur. The first trajectory (yellow) has a corrected length of 0.29 μm and resembles a compact object. The second trajectory has a corrected length of 1.03 μm and represents an elongated object. Error bars on pulse length are based on goodness of fit to predicted pulse shape (supplemental Methods). (E) Positive control showing histogram of PULSIS-determined lengths of double stranded M13 DNA plasmid both in supercoiled (blue) and linearized (red) state at 50 dyn/cm2, imaged in sucrose buffer. Histograms are of motion blur–corrected lengths of hundreds of single molecules. The examples (trajectories and analysis) from Figure 2C and D are 2 statistics from the linearized (red) distribution. Histograms are displayed along with kernel density estimates. Kernel density estimation is a method for smoothing histograms by applying a Gaussian kernel to each point.38 A Gaussian kernel was used with bandwidth set by the Silverman rule.39 (F) Negative control showing kernel density estimate for PULSIS motion blur–corrected beads at different shear stress (manufacture determined diameter of 0.11 μm). Raw histograms are shown in supplemental Figure 1. Number of measurements and mean length and standard deviation for each condition are shown in panels E and F.
Image analysis
PULSIS trajectories were analyzed with custom MATLAB scripts. Trajectories were manually selected, streak lengths were measured, and pulse duration (1,2,3) was assigned. A linear regression of pulse duration and measured lengths with fitting errors was performed, giving the particle velocity (slope) and the corrected molecule length (y-intercept).
Simulation
VWF multimers are represented by spherical beads, connected by a finitely extensible nonlinear elastic potential with relevant hydrodynamic interactions.23 Bead positions are updated according to a discretized Langevin equation based on the applied forces and random fluctuations from Brownian motion. The simulation uses a nonspecific LJ potential, which accounts for a cohesive monomer-monomer attraction and excluded volume. (supplemental Methods, section 2).
Results
PULSIS
To resolve the discrepancy between force scales of free and tethered VWF experiments, we developed a new single-molecule approach to investigate the length response of free VWF to shear flow. The primary experimental challenge was to accurately measure the lengths of molecules rapidly flowing through the field of view. The movement of molecules during image exposure causes motion blur, which is difficult to distinguish from molecule extension.
To correct motion blur at high shear rates, we developed PULSIS, which images each molecule multiple times using a series of different duration laser pulses (Figure 2A and B). The pulse pattern creates a series of fluorescent streaks that encode the length and velocity (dependent on distance from the vessel wall) of the molecule within a single frame. Based on the pulse duration and measured streak lengths, a linear regression gives the particle velocity (slope) and the length for a “zero-duration” pulse (y-intercept), that is, the true length of the molecule. Example experimental PULSIS trajectories (Figure 2C) show a fluorescently labeled DNA molecule flowing across a single frame illuminated with the laser pulse pattern. The measured streak lengths at the corresponding pulse durations are fit to a line (streak length vs pulse duration), with the corrected extension given by the y-intercept (Figure 2D). The corresponding linear fits of the image trajectories in Figure 2C show linearized M13 DNA captured in 2 different orientations that differ in apparent length during tumbling in shear flow.
To test whether PULSIS can distinguish between compact and elongated particles, we measured fluorescently labeled double stranded DNA, in both the supercoiled and linearized states (Figure 2E). Each molecule gave a motion blur–corrected length; these were aggregated together to build up a distribution of lengths (Figure 2E). For example, the 2 trajectories (Figure 2C and D) were single statistics from the distribution for linearized DNA in Figure 2E. Supercoiled DNA remained compacted, giving a normal distribution with mean length L = 0.26 ± 0.25 μm. By contrast, linearized DNA had a broader distribution, with molecules up to ∼1.7 μm and a shifted mean length L = 0.58 ± 0.38 μm, comparable with expected distributions for DNA in shear flow.40 Broadening of the length distribution arises from the rotational component of shear flow, which causes polymers to tumble in cycles of extension and relaxation,41 with sampling of these states resulting in a broad distribution. To further validate PULSIS, fluorescent beads were imaged at shear stresses between 20 and 200 dyn/cm2 (Figure 2F, supplemental Figure 1). The average measurement at each shear stress was within 10 nm of the manufacturer’s reported diameter of 110 nm and had no dependence on the applied shear stress.
Distinguishing collapsed vs extended free VWF can be difficult due to motion blur. One approach imaged fiduciary beads to subtract out motion blur effects for VWF in shear flow.22 However, small deviations in distance from the flow vessel wall between molecules and their fiducials (even less than the depth of field; supplemental Methods, section 3) can result in large errors in perceived VWF length. By contrast, PULSIS uses each molecule as its own reference, without requiring comparison with other objects or precise knowledge of the distance from the surface. Another approach used single short-illumination pulses to minimize the motion blur of VWF in flow.42 However, this method has limited signal-to-noise ratio and retains some motion blur artifacts. By contrast, PULSIS can fully account for motion blur by extrapolation to infinitesimally short pulses while maintaining a strong signal-to-noise ratio. Although others have used short, stroboscopic pulses to limit motion blur and track molecules,42–44 to our knowledge, PULSIS is novel in using a pattern of different duration pulses to measure molecule lengths in flow.
In addition, we used a 60% (w/w) sucrose solution to increase the viscosity of the imaging buffer by ∼58 times compared with water45 to study higher shear rates. This high-viscosity buffer applies equivalent shear stress at a 58-fold lower flow rate with correspondingly lower motion blur.6,42 Surface-tethered VWF was imaged in both aqueous buffer and high-viscosity sucrose buffer at equivalent applied shear stresses (supplemental Figure 2).6 Similar to previous studies,7 no differences in length were observed between molecules in the aqueous and sucrose buffer at the same shear stress, suggesting sucrose has minimal effects on the energetics of VWF extension. With the sucrose buffer and PULSIS, we can measure the lengths of free VWF molecules at shear stresses up to 200 dyn/cm2, double the limit of previous experiments.42
Measurement of free VWF in shear flow
Purified, fluorescently labeled VWF molecules were imaged with PULSIS at shear stresses of 20 to 200 dyn/cm2 (Figure 3A), ranging from low arterial to pathological shear stresses.46 Above 200 dyn/cm2, the signal-to-noise ratio was too low for reliable data. However, this is still twice the highest shear stress imaged in previous studies of VWF free in flow.42 The underlying size distribution of VWF was estimated based on the length of the tethered VWF molecules, with some molecules at least 6 μm in length (supplemental Figure 2B).
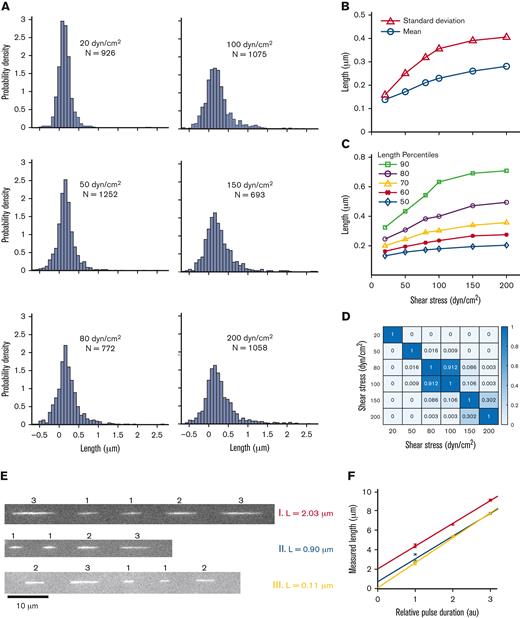
Free-in-flow VWF extension in shear flow. (A) Histogram of VWF length at 6 shear stresses (20, 50, 80, 100, 150, and 200 dyn/cm2). (B) Mean extension vs shear stress (ο) and standard deviation vs shear stress (Δ) of VWF molecules for histograms shown in panel A. Monotonic increases in mean and standard deviation are both consistent with molecules extending under flow. (C) Percentiles 50 to 90 of VWF length vs shear stress for histograms in panel A. (D) Nonparametric statistical significance testing using Mann-Whitney U test comparing each shear stress length distribution. Values for P < .05 indicate statistical significance. (E) Three example trajectories of VWF at 150 dyn/cm2 with different PULSIS-corrected lengths. Example molecules of a long, middle, and short extended molecule. (F) Corresponding plots of pulse length vs relative pulse duration for trajectories in panel E. The y-intercept represents motion blur–corrected lengths for VWF molecules.
Free-in-flow VWF extension in shear flow. (A) Histogram of VWF length at 6 shear stresses (20, 50, 80, 100, 150, and 200 dyn/cm2). (B) Mean extension vs shear stress (ο) and standard deviation vs shear stress (Δ) of VWF molecules for histograms shown in panel A. Monotonic increases in mean and standard deviation are both consistent with molecules extending under flow. (C) Percentiles 50 to 90 of VWF length vs shear stress for histograms in panel A. (D) Nonparametric statistical significance testing using Mann-Whitney U test comparing each shear stress length distribution. Values for P < .05 indicate statistical significance. (E) Three example trajectories of VWF at 150 dyn/cm2 with different PULSIS-corrected lengths. Example molecules of a long, middle, and short extended molecule. (F) Corresponding plots of pulse length vs relative pulse duration for trajectories in panel E. The y-intercept represents motion blur–corrected lengths for VWF molecules.
At the lowest shear stress, the measured length distribution was Gaussian with mean and standard deviation L = 0.15 ± 0.17 μm. We interpreted this distribution as containing compact VWF molecules, with the variance resulting primarily from measurement error. At 50 dyn/cm2, the measured mean increased from 30 nm to 0.18 μm, dramatically less than the ∼10 μm increase suggested22 (Figure 3B). At 200 dyn/cm2, the highest shear stress measured, the mean length had shifted to 0.29 μm. Between 20 and 200 dyn/cm2, the standard deviation increased from 0.16 to 0.41 μm, indicating the distributions were broadening. Similar to linearized DNA, the length distributions broaden at higher shear stresses as the VWF tumbles. The distributions are convolutions of the measurement error, underlying VWF size distribution, and tumbling of individual molecules.
The distributions at each shear stress were compared using the nonparametric Mann-Whitney U test for statistical significance. The test calculated the probability that the length distributions at 2 given shears were the same (Figure 3D). Distributions at similar shear (80 dyn/cm2 vs 100 dyn/cm2) were statistically similar (P = .91). Large changes in shear stress, for example, 50 vs 150 dyn/cm2, gave statistically different distributions (P < .001), indicating the length distribution changed a marginal but statistically significant amount over the shear range explored.
We observed a small population of VWF molecules with a measured length of ∼2 μm (Figure 3A, E and F), consistent with length heterogeneity in the VWF concatemers and suggesting some elongation in this subset at 100 to 200 dyn/cm2. Comparing the 90th percentile of lengths between the 20 and 200 dyn/cm2 shear stresses demonstrated a doubling in length (350-800 nm), whereas the median length changed by <100 nm (Figure 3C).
Brownian dynamics polymer simulations for VWF
Previous attempts to model VWF in flow have relied on coarse-grained Brownian dynamics polymer simulations, as the massive size of VWF and the long timescales of physiological processes make full molecular dynamics simulations unfeasible. The original free VWF in shear studies put forth a widely used Brownian dynamics model.23 With more single-molecule experiments for VWF, we now have orthogonal experiments to test the model against.6,25,42
The 2 parameters u (LJ interaction strength) and r (bead radius) make up a phase space, which represents possible realizations of the simulation (Figure 4A). Used to model basic intermolecular interactions,47 the LJ potential is nonspecific, meaning beads interact with all other beads. The LJ well depth determines the strength of intermolecular interactions. With a large value (u > 0.314 kBT), beads favorably interact to form a collapsed globule resistant to extension up to a critical shear stress, above which a sudden globule-stretch transition occurs.23,30,35 VWF was proposed to behave similar to a collapsed polymer because a sharp transition was reported to occur in shear flow.22 The simulation has been updated in more recent work to include features such as A2 unfolding but continues to use collapsed polymers with LJ potentials between 0.52 and 1.44 kBT.24–26,29,48
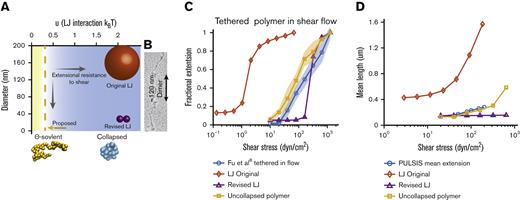
Comparison of Brownian dynamics models for VWF. (A) Parameter space of the simulation as a function of bead diameter and LJ interaction strength. Comparison with the size of spheres representing monomers of the different models. Sizes of spheres are on the same scale as panel B. Blue space represents collapsed polymers, with yellow being uncollapsed polymers. Dotted line represents the ϴ-point, in which the attractive and repulsive forces cancel out. (B) Electron microscopy images of VWF adapted from Fowler et al.49 (C) Comparison between Brownian dynamics simulation and experimental steady state extension for surface-tethered polymers under shear flow. The 3 models are the original LJ model (◇), the revised LJ model (Δ), and the uncollapsed polymer model (□). Simulations compared with experimental data from previous surface stretching experiments of 2- to 3.5-μm VWF molecules from the study by Fu et al (ο, 156 molecules measured).6 For each model and shear stress, the equilibrium extension of 5 independent simulations were averaged together at each shear stress. Extension is normalized by maximum extension and plotted on a semi–log plot. Shaded area shows standard deviation of the 5 simulations. (D) Comparison of Brownian dynamics simulation and experimental mean extension for free-in-flow VWF, with applied shear flow as measured by PULSIS, plotted on a semi–log plot. Because the contour length of the experimental data is unknown, simulations and data are not normalized. Polymer simulation extensions were averaged over a time window and independent runs. (LJ original runs = 3, revised LJ runs = 3, and uncollapsed polymer runs = 10). Absolute contour length of all simulations was ∼3 μm.
Comparison of Brownian dynamics models for VWF. (A) Parameter space of the simulation as a function of bead diameter and LJ interaction strength. Comparison with the size of spheres representing monomers of the different models. Sizes of spheres are on the same scale as panel B. Blue space represents collapsed polymers, with yellow being uncollapsed polymers. Dotted line represents the ϴ-point, in which the attractive and repulsive forces cancel out. (B) Electron microscopy images of VWF adapted from Fowler et al.49 (C) Comparison between Brownian dynamics simulation and experimental steady state extension for surface-tethered polymers under shear flow. The 3 models are the original LJ model (◇), the revised LJ model (Δ), and the uncollapsed polymer model (□). Simulations compared with experimental data from previous surface stretching experiments of 2- to 3.5-μm VWF molecules from the study by Fu et al (ο, 156 molecules measured).6 For each model and shear stress, the equilibrium extension of 5 independent simulations were averaged together at each shear stress. Extension is normalized by maximum extension and plotted on a semi–log plot. Shaded area shows standard deviation of the 5 simulations. (D) Comparison of Brownian dynamics simulation and experimental mean extension for free-in-flow VWF, with applied shear flow as measured by PULSIS, plotted on a semi–log plot. Because the contour length of the experimental data is unknown, simulations and data are not normalized. Polymer simulation extensions were averaged over a time window and independent runs. (LJ original runs = 3, revised LJ runs = 3, and uncollapsed polymer runs = 10). Absolute contour length of all simulations was ∼3 μm.
At smaller interaction potentials (u < 0.314 kBT), a polymer behaves as an uncollapsed polymer. At the ϴ-point (u = 0.314 kBT), the attractive and repulsive forces cancel out, and the polymer’s dimensions match that of a simple ideal chain.50,51 Unlike a collapsed polymer, an uncollapsed polymer’s extension changes smoothly with increasing shear and does not have a sharp transition.41,52
Shear resistance is also dependent on bead size. Larger beads experience more hydrodynamic drag than smaller beads causing elongation at lower shear stresses. In the original model, a large monomer attraction was used to get a sharp transition, which required a large bead of r = 80 nm to fit the critical shear stress. Based on electron microscopy images from Fowler et al49 (Figure 4B) and X-ray crystallography structures,1 a spherical radius of 80 nm overestimates 2 dimensions of VWF monomers. Recent models have attempted to correct this and reduced the bead radius to r = 10 to 15 nm24–26,29,48 but still overestimated the cross-section of VWF monomers (Figure 4B).
We tested a polymer at the ϴ-point (u = 0.314 kBT) and optimized the bead size to best match the single-molecule experiments described in further sections and found a radius of r = 3.7 nm. This radius would require 8 spherical beads to make up a full monomer of 60 nm.49 Notably, this bead size is similar to the size of the 11 domains in each VWF monomer, which range from 1.5 to 3 nm in radius.1,53 We also evaluated the original Brownian dynamics model (u = 2.08 kBT, r = 80 nm)22,23 and a revised LJ model (u = 2.08 kBT, r = 14 nm) with a smaller radius representative of recent models.24–26,48 The simulations are compared with 3 single-molecule experiments: previous measurements of surface-tethered VWF stretching in shear flow and subsequent relaxation6 and measurements here of free VWF in shear flow. All simulations have a contour length of ∼3 μm based on the average maximum extension length from surface extension experiments (supplemental Figure 2B; expanded lengths in supplemental Figures 3, 4, 7, and 9).
Polymer simulations for surface-tethered VWF in shear flow
Surface-tethered VWF in shear flow was simulated with the 3 models described earlier. Experimental data from the study by Fu et al6 show that VWF extends little between 10 and 40 dyn/cm2. Between 40 and 1280 dyn/cm2, VWF requires an exponential increase in shear to achieve a linear length increase. Shear flow was applied to the tethered polymer models, then length in the flow direction was recorded and normalized by the length at the highest shear stress. When normalized by maximum extension, shear-extension curves of VWF are generally independent of length.6
With a small bead size, our uncollapsed polymer experiences less hydrodynamic extensional force than other models, and entropic effects are sufficient to resist extension without a cohesive potential. Similar to VWF, the simulated uncollapsed polymer’s fractional extension scales logarithmically with shear stress and matches the data well (Figure 4C). By contrast, due to the large beads, the original LJ model unfolds completely by 10 dyn/cm2 when tethered to the surface, at a shear stress ∼100 times lower than experimentally observed. Furthermore, independent of bead radius, models with strong LJ interactions extend abruptly over a narrow range of shear stresses.23,35 The revised LJ model was optimized to reach the proper half-maximal extension at the same shear as VWF. This collapsed polymer extends ∼65% of its maximal length between 160 and 320 dyn/cm2, showing an abrupt transition not experimentally observed.
Polymer simulations for free VWF in shear flow
The polymer simulations were further compared with our experimental measurements here of free VWF in shear flow. Shear flow was applied and the length distribution over time was recorded, as measured by the maximum length difference along the axis of flow. Because the contour length of the experimental VWF data was not known, the lengths were not normalized. The experimental data also represented a heterogenous distribution of sizes, making direct comparison difficult as polymer simulations have shown a size dependence for elongation in shear stress.30,54 However, the qualitative behavior of each model was still informative.
Mean extensions of the simulated polymers in free shear were compared with the mean experimental length measurements (Figure 4D). The original LJ model was specifically designed to exhibit large conformational changes in mean extension at shear stresses around 50 to 80 dyn/cm2 and predicted a mean length change of 0.8 μm. The revised LJ model, with parameters set to match the experimental surface stretching data, has a critical shear rate higher than the experiment and shows no change in mean length in the tested range. Our uncollapsed polymer model increases in mean extension by ∼150 nm between 40 and 160 dyn/cm2, qualitatively matching the observed behavior. Based on the uncollapsed polymer model, the mean tension under physiological shear stress was estimated to be <0.1 pN (supplemental Methods, section 4; supplemental Figure 5).
Polymer simulations for VWF relaxation
Polymer relaxation in the absence of flow provides orthogonal experimental VWF data to further test the predictions of models. Relaxation provides details on timescale and conformation. Experimental data were analyzed from the study by Fu et al,6 in which the VWF in a high-viscosity sucrose buffer is hydrodynamically stretched by a high shear stress and imaged as the molecule relaxes. Even in high-viscosity buffer, VWF relaxes quickly in ∼1 second. In our simulations (supplemental Methods, section 5), we found that the relaxation timescale is inversely correlated with the polymer bead size, consistent with a small bead radius to parameterize VWF (supplemental Figures 6 and 7). Furthermore, the relaxation conformation, based on the experimental fluorescence distribution of VWF, disagreed with the collapsed polymer simulation but was well modeled by our uncollapsed polymer simulation (supplemental Figures 8 and 9).
Discussion
We developed PULSIS, an approach for measuring the lengths of molecules in high shear flow by measuring each molecule multiple times with different duration pulses. We then investigated VWF at shear stresses ranging from 20 to 200 dyn/cm2, representing physiological to pathological shear stresses to capture relevant changes in vivo.20 Qualitatively, the VWF length distribution showed no sharp globule-stretch transition near the previously reported 50 dyn/cm2 threshold. Quantitatively, the change in mean length between 20 and 200 dyn/cm2 was 2 orders of magnitude less than the previously reported values (0.17 vs 13 μm).22 This discrepancy may have resulted from motion blur artifacts in the previous work.22 High shear rates coupled with limited axial resolution would make it difficult to account for motion blur with fiducial beads.
The small response of VWF to pure shear flow is a departure from the current perception within the field but still consistent with a majority of VWF literature. Length distributions, with a long tail with low micrometer lengths, is consistent with VWF free-in-flow experiments from the study by Vergauwe et al42 Furthermore, the measured mean extension of free VWF was less than the extension of tethered VWF reported by Fu et al6 at the same shear stress, resolving the force paradox discussed in Figure 1B. A small response of VWF to shear stress was also consistent with small-angle neutron-scattering experiments,55 which found no large-scale rearrangement at 30 dyn/cm2 as well as dynamic light scattering experiments,7 which found no evidence for individual VWF extension at 60 dyn/cm2.
Tension allosterically activates VWF binding to platelet proteins GPIb.6 Furthermore, VWF cleavage by ADAMTS13 requires unfolding of the A2 domain for monomer cleavage, indicating that tension helps regulate VWF function.16 Our results imply that the tension experienced by free VWF in shear flow is lower than previously assumed; as tension depends on the difference in velocity between opposing ends of the molecule, a smaller extension should result in a comparably smaller tension.56
Studies have observed VWF cleavage accelerated with shear stress.17,57 However, other studies have observed no increase in ADAMTS13 cleavage with either high shear or elongational flow58 but find that high turbulent flow results in VWF cleavage.59 Based on our polymer model, the average tension at 80 dyn/cm2, high arterial stress, is estimated to be <0.1 pN (supplemental Figure 5), much lower than the force scale measured for A2 unfolding (fb = 1.1 ± 0.2 pN).16 The estimated tension predicts that physiological shear does not dramatically bias on average the unfolded form of free-VWF A2 for VWF cleavage. However, it is unconfirmed whether physiological force could still play a role in accelerating the rate of cleavage or create a preference for cleavage of longer VWF molecules. The exact flow conditions and contributions from blood proteins such as Factor VIII60 needed for VWF cleavage require further experimental investigation.
VWF localizes to the area of vascular injury and recruits other clotting factors such as platelets. VWF localization is likely driven by binding to collagen in the vessel wall that is exposed in injury.1 Both flow-dependent12 and flow-independent61,62 VWF-collagen binding have been reported. Injury could expose collagen in the endothelium, allowing binding independent of flow. If the VWF-collagen binding rate has some tension dependence, shear stresses <200 dyn/cm2 are not predicted to have a significant role in accelerating binding. Supporting this, Colace and Diamond12 observed minimal rates of VWF-collagen binding at a shear stress of 125 dyn/cm2.
Extension and tension (∼20 pN)6 are necessary to shift the VWF A1 domain from a low affinity to a high affinity state for platelet protein GP1b binding.6 Our results suggest that single molecules of free VWF alone do not exhibit shear stress–dependent binding to GP1b at physiological shear rates. Recruitment of platelets is likely only after VWF is attached to a surface, where the flow directly stretches VWF and higher tensions are reached. Interestingly, Nesbitt et al63 predominantly observed platelet aggregation on vessel walls at the point of stenosis, supporting the idea that both high flow and surface attachments are important for platelet aggregation.
We found no evidence for the sharp transition for free-in-flow VWF predicted by the LJ collapsed polymer simulations. Furthermore, based on the relaxation conformation and surface stretching behavior, the LJ collapsed polymer is not a suitable model for VWF. Meanwhile, our uncollapsed polymer model was consistent with previous VWF surface stretching-in-flow experiments,6 our own PULSIS data for free polymers in shear, and both timescale and conformation of relaxation from a stretched state. Although the good agreement of single-molecule experiments with our uncollapsed polymer models does not constitute proof, an uncollapsed polymer is a sufficient description of the observed mesoscopic VWF dynamics in flow. Optimal bead size is on a similar scale as VWF domains, giving further agreement with physical observations of VWF. Our model suggests that VWF does not adopt a globular, collapsed form, and monomers have minimal attractive interactions. This supports recent ultracentrifuge experiments, in which VWF behaved like a random coil36 and was consistent with the electron microscopy images of VWF.49
The molecular mechanism of VWF activation is based on large conformational changes above a critical shear threshold to initiate hemostasis. However, we found no experimental evidence for a critical shear for large conformational changes in free-in-flow VWF; observed length changes are ∼10 times smaller than previously thought. We found that gradual length changes over a range of shear stress, consistent both in scale and shape with an uncollapsed polymer. Our results suggest that free-flowing VWF molecules cannot act as a responsive sensor of shear stress for activation of hemostasis, invalidating a commonly held view of VWF activation. The field should investigate alternative initiation mechanisms, including the role of elongational flow near constriction sites, flow-independent binding to collagen in the vessel wall, and interaction with platelets.
Acknowledgments
The authors acknowledge the Harvard Medical School Orchestra 2 cluster for computing time. They also thank Fu et al for providing the data.6
This work was supported by funding from the National Institutes of Health (NIH), National Institute of General Medical Sciences (NIGMS) grant R35 GM119537 (W.P.W), National Heart, Lung, and Blood Institute grant HL148755 (T.A.S.), and Molecular Biophysics Training Grant (NIH/NIGMS T32GM008313) (H.T.B).
Authorship
Contribution: H.T.B., W.P.W., Y.J., and D.Y. designed the research; H.T.B. and Y.J. performed the experiments; H.T.B. and D.Y. ran the simulations; W.P.W. and H.T.B. drafted the manuscript; W.P.W., D.Y., Y.J., and H.T.B. analyzed the data; and H.T.B., Y.J., D.Y., T.A.S., and W.P.W. discussed the results and commented on the manuscript.
Conflict-of-interest disclosure: The authors declare no competing financial interests.
Correspondence: Wesley P. Wong, Center for Life Science, Boston Children’s Hospital, 3rd floor, 3 Blackfan Cir, Boston, MA 02215; e-mail: wesley.wong@childrens.harvard.edu.
References
Author notes
Data are available on request from Wesley P. Wong (wesley.wong@childrens.harvard.edu).
The online version of this article contains a data supplement.
There is a Blood Commentary on this article in this issue.
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal