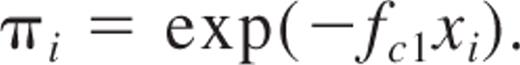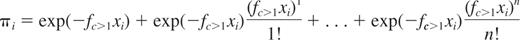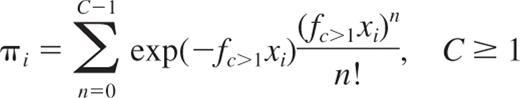Accurate hematopoietic stem cell frequency estimates by fitting multicell Poisson models substituting to the single-hit Poisson model in limiting dilution transplantation assays

Although limiting dilution transplantation assay (LDTA) in recipient animals coupled to the single-hit Poisson model (SHPM) is considered as one of the best methods for quantitating hematopoietic stem cells (HSCs),¹  investigators should be aware of the potential problems associated with this assay.²  In particular, HSC frequency estimates traditionally rely on the SHPM,^1,3  which posits that one donor HSC is sufficient to generate a progeny of detectable differentiated cells above a threshold value in hosts, usually considered approximately 1% of donor-derived cells as estimated by flow cytometry.²  It turns out that the reliability of HSC frequency estimates is critically dependent on this hypothesis. Indeed, it is perfectly acceptable that the progeny of one HSC may be unable to reach this limit of detection imposed by standard flow cytometric analysis. In this context, several recipients having received one, or even more than one, HSC(s) may be falsely classified as negative for reconstitution. This potential situation disqualifies the use of the SHPM. To address this problem, we demonstrate that it is possible to accurately quantitate HSCs, providing that the traditional SHPM is mathematically remodeled to turn to a new class of Poisson models termed multicell Poisson models (C_≥1PMs), which take into account the possibility of recipients misclassified as negative. The validity of this new modeling approach is demonstrated by reassessing 8 previously published LDTAs^4,5  aimed at comparing HSC frequencies in Hoxa-9^−/− versus wild-type mice (2 LDTAs)⁴  and in Notch ligand–stimulated versus –unstimulated CD34⁺ cord blood cells (6 LDTAs).⁵  In 7 of the 8 reanalyzed LDTAs, C_≥1PMs plausibly compete with the traditional SHPM, leading to significant changes in HSC frequency estimates compared with the SHPM.

Details of the LDTAs numbered 1a (Hoxa-9^−/− mice), 1b (wild-type mice), and 2a to 2f (Notch ligand–stimulated CD34⁺ cells and controls) are described in supplemental Tables 1 and 2 (available on the Blood Web site; see the Supplemental Materials link at the top of the online article).^4,5 

The equation of the SHPM model is as follows:

This is the first term in the Poisson series, describing the equation of the SHPM.^3,6  In this equation, π_i is considered as the proportion of the recipient population with no detectable donor-derived blood cells (negative outcome), f_c1 is the HSC frequency estimate, and x_i is the number of cells at each cell dose group i with i = 1, 2, …, k, where k is the total number of cell doses. The major assumption of the SHPM is that only animals that receive zero HSCs do not produce positive outcome, whereas animals transplanted with 1, 2, …, C HSC(s) will result in positive outcome.

The general equation of the models of the class of C_≥1PMs is as follows:

This equation describes a series of more sophisticated Poisson models that extend the basic SHPM by including the second term, third term, …, nth term of the Poisson series in addition to the first term of the Poisson series, where f_c>1 is the HSC frequency estimate. This equation can be written as follows:

It describes the general form of the multicell PMs (C_≥1PMs). C appears for each model as the minimum number of HSCs necessary to promote a detectable positive outcome. A set of 20 models is tested, C taking the value 1, 2, …, 20. The C_≥1PMs include the SHPM (C = 1) but leave open the possibility that more than one HSC (C > 1) is necessary to give rise to a progeny of detectable differentiated cells in transplanted animals (positive outcome). In the case where C > 1, our hypothesis is that C_≥1PMs mathematically capture the situation in which a proportion of recipients having received HSC(s), but not in sufficient number (ie, 1 to C − 1), have been falsely scored as negative outcome.

In a previously published paper,⁷  we advised a statistical test aimed at estimating the fit of the SHPM to the data and based on a generalized linear modeling approach. Briefly, testing the null hypothesis that the slope β is equal to 1 (β = 1) explores the SHPM hypothesis, and this can be performed by a standard likelihood ratio test.⁸  Standardized deviance residuals⁹  were also used as SHPM checking diagnostics after fitting the SHPM³  to the LDTAs.

Calculations of C_≥1PM-based HSC frequencies were obtained by a standard maximum likelihood procedure applied to binomial data.⁹  Comparison of the C_≥1PMs models was performed with Akaike information criterion (AIC) and the related Akaike weights, called w, grounded on an extension of the AIC known as information-theoretic approach, applied to model uncertainty and multimodel inference.^10-15  Finally, C_≥1PM-based HSC frequency estimates were averaged across the set of all plausible C_≥1PMs, along to a statistical procedure that takes into account the HSC frequency estimates and the relative Akaike weights of all plausible C_>1PMs^10,11  (supplemental Methods).

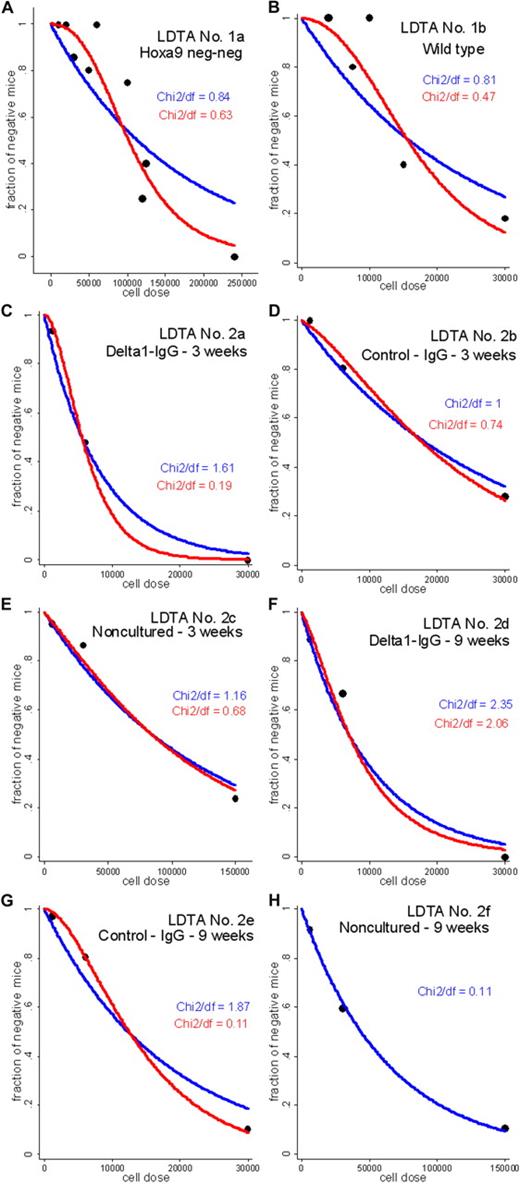
The SHPM is rejected for the LDTA nos. 1a, 2a, and 2e (P < .05) and is barely acceptable for the LDTA nos. 1b and 2d (P < .1; supplemental Table 3), casting doubt on the accuracy of the previously reported HSC frequency estimates^4,5  for these 5 of the 8 LDTAs. The standardized deviance residuals under the SHPM are presented in supplemental Figure 1A-B. Overall, it can be observed that the residuals are usually positive at low cell doses and negative at high cell doses. Given the structure of the deviance residuals,⁹  this means that the fraction of negative mice under the SHPM tends to be underestimated at low cell doses and overestimated at high cell doses. The occurrence of such a systematic pattern favors the hypothesis that the SHPM is not correct and motivates the development of alternative Poisson models. Next, C_≥1PMs are fitted to the LDTA data with C taking the values 1 to 20. Based on the log-likelihood values, it can be computed AIC, ΔAIC_m (the AIC difference between the best model and a given model in the set), and weights w that represent the probability of each model to be the expected best model (Supplemental data); a representative example of calculation is given in supplemental Table 4. Based on each Akaike weight w, it can be observed that the best model probability w obtained for a given C_≥1PM is not large relative to the weights for the other competing C_≥1PMs (supplemental Figure 2 left panels). The conclusion is that there is no model from the C_≥1PMs, including the traditional SHPM, that can be considered as the best-approximating model to the data, except in LDTA no. 2f exhibiting w close to 1 for the model with C = 1, strong evidence that the SHPM is the expected best model. Considering this model uncertainty for 7 of the 8 LDTAs, HSC frequency estimates f̃ were computed by a model averaging procedure across the plausible C_≥1PMs, defined as the set of models with ΔAIC_m ≤ 10 (supplemental Figure 2 right panels). C_≥1PM-averaged HSC frequency estimates f̃ are higher than HSC frequency estimates f_c1 based on the SHPM, with 1.32- to 5.88-fold increases (Table 1). Fitted SHPM and C_≥1PMs regression lines for the 8 LDTAs are presented in Figure 1A-H, with χ²/df ratios (χ²-dispersion statistics; supplemental data) favoring the conclusion that C_>1PMs fit better to the data than the SHPM. This study strongly suggests that C_≥1PMs should be routinely used to more accurately estimate HSC frequencies in LDTAs. In line with our main finding that a single HSC may not be sufficient to generate detectable hematopoietic reconstitution in recipients, single-cell transplantations performed with various HSC-enriched populations may have chronically underestimated the total HSC frequencies.¹⁶ 

This work was supported by Association pour la Recherche sur le Cancer (grant 3218).

Contribution: T.B. performed mathematical and statistical data modeling; and M.C. and T.B. cowrote the paper.

Conflict-of-interest disclosure: The authors declare no competing financial interests.

Correspondence: Thierry Bonnefoix, Inserm, U823, Oncogenic Pathways in the Haematological Malignancies, Institut Albert Bonniot, Grenoble Cedex 9, France; e-mail: thierry.bonnefoix@ujf-grenoble.fr.