With great interest we read the article by Quesenberry et al1 on the chiaroscuro stem cell. Based on many experimental findings that contrast the classical paradigm of a stem cell hierarchy with irreversibly declining proliferative potential, the authors formulate a new qualitative concept of a nonhierarchical, flexible stem cell behavior.
As the stem cell definition is still a functional one,2,3 requiring a checking by different assays, it is necessary to show for any concept whether it conforms with the list of qualifying criteria. In this context we like to draw attention to the possibility of formulating a quantitative theory. Recently, we have described a novel quantitative model of stem cell organization3,4 that has conceptual similarities to the concept proposed by Quesenberry et al. The model is based on the concept of within-tissue plasticity, assuming that particular cellular properties can reversibly be acquired or lost, and quantitatively changed within a range of potential options. The decision of whether a property is expressed or not and to which degree depends on the current state of the cell and on the microenvironmental signals that it is able to recognize. Using a simulation model we can show that such a functional view on cellular organization can consistently explain a broad variety of experimental observations on heterogeneity and plasticity of cellular properties and functionalities in the hematopoietic system with full conformity to all the functional stem cell criteria.4
Quesenberry and colleagues relate the observed phenotypic plasticity (summarized in the term “chiaroscuro”) mechanistically to cell cycle activity. In contrast, in our model plasticity is not directly linked to cell cycle activity, but cell cycle activation results from a switching of cells between different growth environments (GEs).
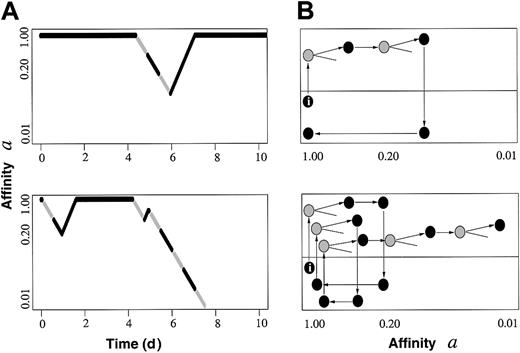
Figure 1 shows simulated time courses of individual cells with respect to a model property a describing the actual affinity of cells to reside in a specific GE that supports the maintenance and renewing of a. Cells in this GE are assumed to be in G0. They can change to another GE where property a is declining while the cell cycle is activated. Lineage commitment (ie, loss of stemness) is entered if a falls below a critical threshold (here, 0.01). The actual value of a can be interpreted as a measure of self-renewal ability, and therefore, of long-term repopulating potential. Figure 1 shows that in our model, changes in cell cycle are associated with reversible changes in the property a.
Simulation examples. (A) Two time courses of individual cells (tracing of one daughter cell per division) with respect to affinity a, showing the actual cell cycle status. Black segments represent cell cycle phases G1/G0, gray segments indicate S/G2/M. Whereas the upper example describes a cell maintaining/renewing a high a (ie, long-term repopulating potential), the lower example shows terminal lineage commitment after several fluctuations. (B) Corresponding cell fates represented in terms of the proposed within-tissue plasticity model4 (I, initiating cell; gray, S/G2/M; black, G1/G0). Dormant cells in lower growth environment (gray region) regain affinity a, whereas (potentially) cycling cells in the other environment (white region) lose a.
Simulation examples. (A) Two time courses of individual cells (tracing of one daughter cell per division) with respect to affinity a, showing the actual cell cycle status. Black segments represent cell cycle phases G1/G0, gray segments indicate S/G2/M. Whereas the upper example describes a cell maintaining/renewing a high a (ie, long-term repopulating potential), the lower example shows terminal lineage commitment after several fluctuations. (B) Corresponding cell fates represented in terms of the proposed within-tissue plasticity model4 (I, initiating cell; gray, S/G2/M; black, G1/G0). Dormant cells in lower growth environment (gray region) regain affinity a, whereas (potentially) cycling cells in the other environment (white region) lose a.
Our theory conforms with Quesenberry's reasoning, but additionally it provides a quantitative reproduction of many other experimental phenomena.4 Furthermore, the model allows to separate emerging phenomena from underlying mechanisms. As an example we refer to the observed differences in the engraftment potential of cell populations sorted for their actual cell cycle status. Quesenberry et al consider these phenomena as evidence for a cell cycle–associated plasticity. Our model does not explicitly assume cell cycle–dependent engraftment advantages. However, it produces a heterogeneous stem cell population with respect to a. Cells from this population selected for G1/G0 exhibit a larger proportion of cells with high a (high long-term repopulating potential) compared to cells selected for S/G2/M.
It has to be emphasized that theoretical modeling cannot prove hypotheses. However, modeling offers the possibility to test the impact of different (latent) molecular and genetic mechanisms on the generation and variability of phenotypic processes emerging in functional assays or in vivo. In this regard we think tissue stem cell modeling is only at its start.
Quantitative tissue stem cell modeling
Roeder and Loeffler comment on our recent paper, “The chiaroscuro stem cell: a unified stem cell theory”1 and describe “quantitative stem cell modeling.” They describe “within-tissue plasticity,” where it is assumed that certain cellular characteristics can be reversibly acquired or lost. They propose that these characteristics can be “quantitatively changed within a range of potentials.” The final phenotype of the cell depends on the state of the cell and the inductive influences of the microenvironment. Our chiaroscuro continuum model shows exactly these characteristics, but in a broader context. One can substitute a cell cycle–related parameter for “state of the cell” and inductive signals for “microenvironmental signals.”
The Roeder-Loeffler model is described in more detail in the referenced Experimental Hematology publication.2 In that article, they assume 2 different growth environments (GE-A, GE-Ω), where each cell is characterized by 2 properties: the cycling status (c) and a property (a), which describes the affinity of the cell to reside in GE-A. Nonproliferative cells reside in GE-A, whereas cells in GE-Ω proliferate. Final outcomes are determined by the interaction of the cells and their microenvironments. This would appear to represent a simple digital model, while our chiaroscuro theory is an analog model with continuously changing potential for the stem cells and its inducers. It is not clear that the within-tissue plasticity model “additionally.... provides a quantitative reproduction of many other experimental phenomena” beyond that offered by the chiaroscuro model. In fact, the chiaroscuro model incorporates a full range of quantitative experimental phenomena and is less limited than the within-tissue plasticity model. In the chiaroscuro model the stem cell phenotype is continuously changing with cell cycle (or some other related phenomena), while the Roeder-Loeffler model proposes 2 discrete stem cell states. Further, our concept of microenvironment includes any inductive influences. We hypothesize that the environmental inductive influences acting on the cell also are continuously changing, rather then being represent by 2 discrete microenvironments.
Despite comments to the contrary, the Roeder-Loeffler model explicitly assumes cell cycle dependence, as illustrated by this quotation: “cells from this population selected for G1/G0 exhibit a large proportion of cells with high a (high long-term repopulating potential) compared to cells selected for S/G2/M.” It's important to acknowledge that parameters other than cell cycle may be operative here, although the correlations between cell cycle phase and phenotype change are very strong. Altogether, the 2 models suggest a new way of viewing hematopoiesis and, in fact, are remarkably similar.
Both models, also, begin to explain the heterogeneity of the most purified stem cell population. This feature has been neglected or denied by many investigators but is critical to an understanding of stem cells. Drs Roeder and Loeffler2 in their Experimental Hematology article cite 4 references for stem cell heterogeneity as to cycling activity, colony-forming ability, and phenotypic markers. We have recently studied the colony-forming and differentiation capacity of highly purified lineage-negative rhodamine low Hoechst low murine stem cells cloned as single cells in response to 7 growth factors. We found virtually total heterogeneity as to colony formation and colony size. When the differentiated cell types in these colonies were determined, 14 different colony types were defined. Recently, in the plasticity debate, many investigators have stated that clonal stem cell experiments are essential for interpretable results in transdifferentiation studies. We quote, “First single cells must be shown to be capable of both the expected and unexpected differentiation.”3 If a defined stem cell population is very heterogeneous, then a clonal study is not meaningful unless thousands of clones are evaluated. This is, of course, a population study. Clonal studies in a heterogeneous population serve to define that heterogeneity but offer little else.
The above models can probably be extended to encompass marrow to nonhematopoietic tissue conversions, that is, stem cell plasticity. We had originally proposed this in the manuscript submitted to Blood, but the reviewers requested its removal. It seems highly unlikely that the concepts represented in these models will not extend to the production of heart, liver, skin, or other cells by marrow stem cells.
We understand the restraints imposed when carrying out mathematical modeling, as was done by the authors in the Experimental Hematology paper.2 Simplicity is an initial requirement. As pointed out by the authors, there are many other variables that will need to be incorporated into their model. Hopefully, these will include the continuously changing phenotype of the marrow stem cell with cycle transit. Given the growing quantity and complexity of information on the stem cell, modeling, such as described here, will become increasingly essential to our understanding of stem cell biology. In our laboratory we have begun to brush up on our basic mathematics, to read calculus, and even to ponder chaos. We have indeed entered the era of stem cell modeling.
Supported by grants P01 DK50222, P01 HL56920, and R01 DK27424.
Correspondence: Peter J. Quesenberry, Center for Stem Cell Biology, Roger Williams Medical Center, 825 Chalkstone Ave, Providence, RI 02908-4735; e-mail: pquesenberry@rwmc.org.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal