Abstract
Moderate intensification of conventional multicycle chemotherapy has recently been shown to improve treatment results in malignant lymphomas and might prove to be beneficial also in other malignancies. However, the feasibility of such regimens is mainly limited by their granulopoietic toxicity. To identify and quantify the basic cell kinetic mechanisms of damage and stimulation caused by cytotoxic drugs and recombinant human granulocyte colony-stimulating factor (rhG-CSF), respectively, we developed a mathematical model of human granulopoiesis that allows simulation of leukocyte concentration profiles under 10 different multicycle polychemotherapy regimens with varying drug composition, dosage, and scheduling, including rhG-CSF assistance. Clinical data on leukocyte profiles were obtained from large numbers of patients treated within several multicenter trials. Simulation studies show that the leukocyte profiles of all regimens can be appropriately fitted using one single set of assumptions and parameters for the cell kinetic effects of cytotoxic drugs and rhG-CSF. Furthermore, the model can be used to explain the interindividual heterogeneity of hematotoxicity by a differential chemosensitivity, which might be useful in drug scheduling for specific risk groups. It is demonstrated that the model can be used to design and to select new drug schedules for subsequent clinical trial testing.
Introduction
Evidence is currently accumulating that moderate dose escalation or intensification of conventional chemotherapies can substantially improve treatment outcome in malignant lymphomas.1-5 However, neutropenia is a frequent adverse effect of such regimens, and it is well known that the risk of bacterial infections increases with the severity, rapidity of development, and duration of neutropenia.6,7 Although comparative clinical studies have shown that prophylactic administration of recombinant human granulocyte colony-stimulating factor (rhG-CSF) can reduce the risk of neutropenic infections and that rhG-CSF permits the maintenance of dose and time intensity, neutropenia remains a major limiting factor for treatment intensification.2,8-11 Therefore, drug doses and application intervals must be chosen in such a way that a tolerable degree of neutropenia will not be exceeded. Ideally, blood cell production should be disturbed as little as possible throughout the entire therapy. The design of intensified regimens fulfilling this demand often requires extensive dose-escalation and feasibility trials.12 To allow a more targeted selection of appropriate regimens for clinical testing, one may wish to predict the leukocyte profile for a specific regimen in advance. However, this task is not straightforward because the observable time course of leukocyte numbers is the complex result of a superposition of different suppressive and stimulatory effects of the drugs on the granulopoietic tissue. To our knowledge, no comprehensive dynamic model of human granulopoiesis is available so far that allows one to simulate the leukocyte dynamics in cyclic polychemotherapy.
Here we addressed this issue by means of a mathematical model of human granulopoiesis. The model is based on current knowledge of the biology of granulopoietic cell proliferation and its regulation. It was our objective to investigate whether the typical leukocyte profiles under various clinical regimens can consistently be explained by a single set of biologically plausible assumptions about the toxic and stimulatory cell kinetic modes of action of the cytostatic drugs and G-CSF, respectively. Furthermore we aimed to make model predictions for yet clinically untested schedule variants.
In the past years, we have been involved in the conduct of a variety of large randomized controlled multicenter trials of the German Hodgkin's Lymphoma Study Group and the German High-Grade Non-Hodgkin's Lymphoma Study Group. These trials were initiated to test the therapeutic efficacy of different intensified and nonintensified conventional multidrug multicycle chemotherapies with and without rhG-CSF support.1,3-5 White blood cell counts have routinely been documented that allowed detailed characterization of the dynamics of leukopenia under these regimens.13,14 Leukocyte data from 10 different regimens were chosen as the paradigmatic basis for this work. The regimens varied regarding drug composition, dosage, and timing of hematotoxic drugs cyclophosphamide, doxorubicin, etoposide, vincristine, procarbazine, and the growth factor rhG-CSF. Additionally, data on the effects of subcutaneous rhG-CSF administration without chemotherapy were obtained from published literature.
Materials and methods
Clinical data
Data on peripheral white blood cell counts (WBCs) during the administration of 10 different multidrug multicycle chemotherapy regimens were taken from clinical trials of the German Hodgkin's Lymphoma Study Group and the German High-Grade Non-Hodgkin's Lymphoma Study Group with kind permission (Table 3). Some trials included only patients younger than 60 years of age, and others considered only older patients. Because the regimens CHOP-21, CHOP-14, CHOEP-21, and CHOEP-14 comprised patients both below and above the age of 60, the data of these regimens were stratified into 2 subgroups to ensure comparability with other protocols. Except for BEACOPP-21-escalated, the adherence to the planned doses was good.13,14
Chemotherapy characteristics
. | . | . | . | Dose, mg/m2/d or mg/d†(days of administration in each cycle) . | . | . | . | . | . | . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regimen . | Patients (WBC measurements) . | Age . | Cycles (cycle duration, d) . | CPH . | DOX . | VIN . | ETO . | PRO . | BLM . | PRD . | G-CSF* . | |||||||
| CHOP-21‡ | 396 (8055) | y/o | 6 (21) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | None | |||||||
| CHOP-14‡ | 393 (8354) | y/o | 6 (14) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | (4-13) | |||||||
| CHOEP-21‡ | 387 (9071) | y/o | 6 (21) | 750 (1) | 50 (1) | 2† (1) | 100 (1-3) | None | None | 100† (1-5) | None | |||||||
| CHOEP-14‡ | 398 (9335) | y/o | 6 (14) | 750 (1) | 50 (1) | 2† (1) | 100 (1-3) | None | None | 100† (1-5) | (4-13) | |||||||
| CHOP-14s, with shortened G-CSF‡ | 374 (7029) | o | 6/8 (14) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | (6-12) | |||||||
| hCHOEP-21‡ | 79 (2824) | y | ||||||||||||||||
| Dose level 1 | 6 (21) | 1000 (1) | 27.5 (1) | 2† (1) | 125 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 2 | 6 (21) | 1200 (1) | 30.0 (1) | 2† (1) | 150 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 3 | 6 (21) | 1400 (1) | 32.5 (1) | 2† (1) | 175 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 4 | 6 (21) | 1600 (1) | 35.0 (1) | 2† (1) | 200 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| hCHOEP-14‡ | 39 (1332) | y | ||||||||||||||||
| Dose level 1 | 6 (14) | 1000 (1) | 27.5 (1) | 2† (1) | 125 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 2 | 6 (14) | 1200 (1) | 30.0 (1) | 2† (1) | 150 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| BEACOPP-21-baseline§ | 430 (11 789) | y | 8 (21) | 650 (1) | 25 (1) | 2† (8) | 100 (1-3) | 100 (1-7) | 10 (8) | 100 (1-14) | None | |||||||
| BEACOPP-21-escalated§ | 399 (15 840) | y | 8 (21) | 1250 (1) | 35 (1) | 2† (8) | 200 (1-3) | 100 (1-7) | 10 (8) | 100 (1-14) | (8-15) | |||||||
| BEACOPP-14§ | 82 (1969) | y | 8 (14) | 650 (1) | 25 (1) | 2† (8) | 100 (1-3) | 100 (1-7) | 10 (8) | 80 (1-7) | (8-13) | |||||||
. | . | . | . | Dose, mg/m2/d or mg/d†(days of administration in each cycle) . | . | . | . | . | . | . | . | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regimen . | Patients (WBC measurements) . | Age . | Cycles (cycle duration, d) . | CPH . | DOX . | VIN . | ETO . | PRO . | BLM . | PRD . | G-CSF* . | |||||||
| CHOP-21‡ | 396 (8055) | y/o | 6 (21) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | None | |||||||
| CHOP-14‡ | 393 (8354) | y/o | 6 (14) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | (4-13) | |||||||
| CHOEP-21‡ | 387 (9071) | y/o | 6 (21) | 750 (1) | 50 (1) | 2† (1) | 100 (1-3) | None | None | 100† (1-5) | None | |||||||
| CHOEP-14‡ | 398 (9335) | y/o | 6 (14) | 750 (1) | 50 (1) | 2† (1) | 100 (1-3) | None | None | 100† (1-5) | (4-13) | |||||||
| CHOP-14s, with shortened G-CSF‡ | 374 (7029) | o | 6/8 (14) | 750 (1) | 50 (1) | 2† (1) | None | None | None | 100† (1-5) | (6-12) | |||||||
| hCHOEP-21‡ | 79 (2824) | y | ||||||||||||||||
| Dose level 1 | 6 (21) | 1000 (1) | 27.5 (1) | 2† (1) | 125 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 2 | 6 (21) | 1200 (1) | 30.0 (1) | 2† (1) | 150 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 3 | 6 (21) | 1400 (1) | 32.5 (1) | 2† (1) | 175 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 4 | 6 (21) | 1600 (1) | 35.0 (1) | 2† (1) | 200 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| hCHOEP-14‡ | 39 (1332) | y | ||||||||||||||||
| Dose level 1 | 6 (14) | 1000 (1) | 27.5 (1) | 2† (1) | 125 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| Dose level 2 | 6 (14) | 1200 (1) | 30.0 (1) | 2† (1) | 150 (1-3) | None | None | 100† (1-5) | (6-13) | |||||||||
| BEACOPP-21-baseline§ | 430 (11 789) | y | 8 (21) | 650 (1) | 25 (1) | 2† (8) | 100 (1-3) | 100 (1-7) | 10 (8) | 100 (1-14) | None | |||||||
| BEACOPP-21-escalated§ | 399 (15 840) | y | 8 (21) | 1250 (1) | 35 (1) | 2† (8) | 200 (1-3) | 100 (1-7) | 10 (8) | 100 (1-14) | (8-15) | |||||||
| BEACOPP-14§ | 82 (1969) | y | 8 (14) | 650 (1) | 25 (1) | 2† (8) | 100 (1-3) | 100 (1-7) | 10 (8) | 80 (1-7) | (8-13) | |||||||
CPH indicates cyclophosphamide; DOX, doxorubicin; VIN, vincristine, ETO, etoposide; PRO, procarbazine; BLM, bleomycin; PRD, prednisone; G-CSF, granulocyte colony-stimulating factor; y, young (younger than 60 years); and o, old (60 years or older).
Subcutaneous administration, 300 or 480 μg/d (depending on body weight).
Doses expressed as mg/d are marked with a dagger.
Part of a trial of the German High-Grade Non-Hodgkin's Lymphoma Study Group.
Part of a trial of the German Hodgkin's Lymphoma Study Group.
The average time courses of WBCs and their variation within the patient populations were characterized by the median and the interquartile range from all available values at each day of therapy. Data on leukocyte profiles in healthy individuals during daily subcutaneous rhG-CSF administration have been taken from the published literature.15-22
Model structure
The following paragraphs give a detailed description of the basic model concept, the regulatory structure, and all assumptions about the modes of action of cytotoxic drugs and G-CSF. However, a complete mathematical presentation of the model would go beyond the scope of this paper. Therefore, mathematical formulas are only shown for the most important assumptions or when necessary for understanding. Our group plans to publish a complete description of the full mathematical details in the future.
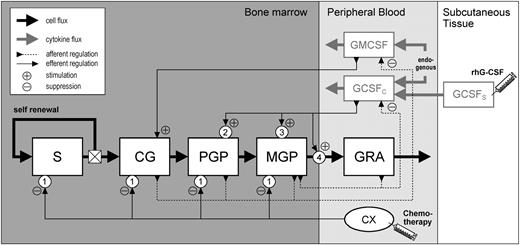
The basic model concept has been derived from previous work of our group on models of murine and particularly human granulopoiesis.23-26 Figure 1 gives an overview of the model structure. The model considers human granulopoiesis as a set of compartments, each representing the population size (ie, cell number) of a distinct hematopoietic cell stage. The compartments are concatenated according to their order of development. Granulopoiesis originates from a stem cell compartment, S, with self-renewal capability. Under steady state conditions, 50% of the cells emerging from S reenter this compartment, and 50% propagate to the next more committed stage. CG represents the most immature progenitor cell stage, granulocyte-macrophage colony-forming unit (CFU-GM). The PGP compartment comprises all morphologically identifiable granuloid precursors still capable of proliferation (myeloblasts, promyelocytes, myelocytes). MGP represents the maturing (ie, postmitotic) precursor pool (metamyelocytes, banded and segmented neutrophils). GRA corresponds to the circulating granulocytes in the peripheral blood. The transitions of cells between the compartments are considered as rates (ie, numbers of cells leaving or entering a compartment per time unit). These rates depend on typical cell kinetic parameters, the 2 most important of which are the transit time, T (the mean time of a cell residing in a compartment), and the amplification, A (which quantifies the increase of cell numbers during development due to mitotic division). Mathematically, each compartment is represented by an ordinary differential equation of the following general type:
The equation describes the change of the compartment size C(t) at any given time as the balance between the influx and efflux rates (where I is the influx and C(t)/T is the efflux, with T being the mean transit time). The amplification parameter, A, multiplies the influx rate due to mitotic divisions (which equals 1 for nonproliferative cell stages and is more than 1 for proliferative cell stages).
Model structure. The compartments S, CG, PGP, MGP, and GRA represent stem cells, CFU-GM, proliferating granuloid precursors (myeloblasts, promyelocytes, myelocytes), maturing granuloid precursors (metamyelocytes, banded and segmented neutrophils), and peripheral neutrophils, respectively. GCSFC and GMCSF indicate the circulating levels of G-CSF and GM-CSF, respectively. GCSFS represents the subcutaneous compartment for exogenous rhG-CSF. CX represents the chemotherapy. Bold black and gray lines indicate cell and cytokine flux, respectively. Thin dashed and solid lines indicate the afferent and efferent parts of regulatory loops, respectively. Numbers in circles indicate the basic modes of drug action: (1) acute loss of cells, (2) enhanced mitotic activity, (3) accelerated differentiation, and (4) increased rate of release to the peripheral blood stream.
Model structure. The compartments S, CG, PGP, MGP, and GRA represent stem cells, CFU-GM, proliferating granuloid precursors (myeloblasts, promyelocytes, myelocytes), maturing granuloid precursors (metamyelocytes, banded and segmented neutrophils), and peripheral neutrophils, respectively. GCSFC and GMCSF indicate the circulating levels of G-CSF and GM-CSF, respectively. GCSFS represents the subcutaneous compartment for exogenous rhG-CSF. CX represents the chemotherapy. Bold black and gray lines indicate cell and cytokine flux, respectively. Thin dashed and solid lines indicate the afferent and efferent parts of regulatory loops, respectively. Numbers in circles indicate the basic modes of drug action: (1) acute loss of cells, (2) enhanced mitotic activity, (3) accelerated differentiation, and (4) increased rate of release to the peripheral blood stream.
Cell transitions between compartments except for the MGP compartment are considered to be independent of cell maturity (ie, the efflux rates follow a first-order kinetic). In contrast, MGP cells are assumed to leave the compartment in a more or less age-dependent fashion mimicking almost a “first in, first out” transition. Technically, this can be approximated by subdividing the compartment into several subcompartments (ie, equations) with simple first-order transitions.
The model incorporates several negative feedback loops for the regulation of cell production. Each loop consists of an afferent and efferent part, which are linked together by a sigmoidal regulatory function with a saturation characteristic. The afferent part carries information about the present system state (ie, the number of cells in the compartments). The efferent part controls the cell kinetic parameters—that is, proliferation (A) and maturation time (T). Two major feedback loops are mediated by the compartments GCSFC and GMCSF, which represent the hematopoietic growth factors G-CSF and granulocyte-macrophage–CSF (GM-CSF), respectively. The GM-CSF feedback loop has been described in detail previously.24,26,27 The efferent part of the G-CSF loop controls the amplification in PGP, the transit time in MGP, and the rate of cells emerging from bone marrow to the peripheral blood. The afferent part of the loop controls the present serum concentration of G-CSF. Experimental findings show that daily subcutaneous injections of rhG-CSF lead to characteristic fluctuations of the serum G-CSF concentration profile in human beings, with maximum concentrations being several orders of magnitude higher than normal.22,28-30 To allow for these fluctuations in the model we assume a simple pharmacokinetic model of rhG-CSF with extravascular administration. The GCSFS compartment represents the subcutaneous rhG-CSF depot from which the drug is transferred to the central GCSFC compartment with a first-order kinetic (quantified by a single absorption coefficient ka). The central G-CSF compartment also gets influx from an endogenous source. The biologic activities of the endogenous and exogenous G-CSF are assumed to be identical. Furthermore, G-CSF is assumed to be removed from circulation by a nonspecific process with an elimination coefficient ku and by a specific process with a rate being proportional to the number of cells in GRA (with a proportionality factor ks). Thus, the balance equation for the central G-CSF compartment is defined as follows:
where G(t) is the present circulating G-CSF level, Iexo and Iendo are the present influx rates due to absorption from the subcutaneous compartment and endogenous production, respectively, and GRArel is the present neutrophil number relative to the normal steady state number.
Mathematically, the complete model is a system of coupled nonlinear ordinary differential equations that can be solved by numeric integration. The model does not compare absolute cell numbers, because they are largely unknown for most bone marrow cell stages even in the normal steady state. Therefore, cell numbers during perturbation are always determined relative to the unperturbed steady state. However, to allow meaningful comparison of relative GRA compartment sizes with absolute leukocyte concentrations, a scaling factor of 7000/μL is applied, which corresponds to the mean leukocyte concentration in healthy individuals.31
The model was realized and solved on a standard personal computer using the numeric computation software MATLAB 5.2.0.3084 and SIMULINK toolbox (The MathWorks, Natick, MA). Previous work of our group has shown that a large number of experimentally induced or disease-related hematopoietic disturbances in the mouse, dog, or human being can be described by this model approach.24-27,32-35
Model assumptions about the cell kinetic effects of cytotoxic drugs
It is assumed that a cytotoxic drug leads to a rapid removal of cells in each bone marrow compartment. The amount of cells being removed per time unit (ie, the cell kill rate) is assumed to be proportional to the number of cells in the compartment. A proportionality factor k characterizes the magnitude of toxicity (hereafter referred to as the “toxicity coefficient”). The toxicity coefficients are specific for each cell stage and depend on the drug type and dosage. Pilot simulations showed that toxicities for the S and CG compartments could not unambiguously be distinguished from each other. Hence, only one coefficient for both cell stages is considered.
No explicit pharmacokinetic model for cytotoxic drugs and their metabolites is considered. According to their short half-life times, cell removal is restricted to a period of 24 hours and then returns to zero. Bleomycin, which is part of the BEACOPP regimen, is assumed not to cause a relevant hematotoxicity. Furthermore, neither a prolonged nor an irreversible damage to hematopoietic cells is assumed. The effects of different drugs given concomitantly are considered by simply adding their toxicity coefficients. These model assumptions lead to the following general extension of the first-described equation (bold letters):
where k1 through kn are the drug- and cell stage–specific toxicity coefficients.
The toxicity coefficients are assumed to be constant over successive therapy cycles except for the first cycle. During simulation of the first cycle all coefficients of toxicity are multiplied by one unique factor ffirst-cycle being more than 1. This assumption is necessary to account for the fact that the granulopoietic system is unperturbed at the beginning of the first cycle, but not at the beginning of all other cycles.
The quantitative relationship between the drug dose and the corresponding toxicity is modeled by a simple nonlinear function of the type k =βDα, with k being the coefficient of toxicity, D being the drug dose, and α and β being parameters characterizing the shape of the nonlinear relationship.
Model assumptions about the cell kinetic effects of G-CSF
G-CSF levels above normal lead to a shortening of the transit time in the MGP compartment, to an increased mitotic cell amplification in the PGP compartment, and to an increase of the rate at which mature leukocytes emerge from the bone marrow to the blood. Vice versa, subnormal levels lead to the opposite effects. For all effects, characteristic dose-response dependencies with a sigmoidal shape are assumed.
Further assumptions
Prednisone is able to increase neutrophil numbers in the peripheral blood. Therefore, it is assumed that prednisone causes a characteristic prolongation of the transit time by 66% in the GRA compartment.36 Advanced stage Hodgkin lymphoma patients showed a markedly higher WBC before the start of treatment, which might be caused by elevations of their G-CSF serum levels.37 We therefore assume a slightly increased endogenous G-CSF production in the model that gradually declines to zero during therapy due to the continuing destruction of the tumor. Furthermore, the leukocytosis caused by the vincristine and prednisone pretreatment in the CHOP-14s regimen is also considered in the model.
Parameter estimation
A major goal was to obtain appropriate values for all coefficients of toxicity and for all other free model parameters (in particular, the G-CSF–dependent regulation process). This parameter estimation was performed through a stepwise iterative fitting of model curves to leukocyte data from the clinical multicenter trials. The purpose was to identify parameter values that lead to the best agreement between the model and clinical data. Evolutionary strategies were applied to identify optimal parameter values.38,39 The error function to be minimized was defined as a weighted sum of the squared differences between the data and model values on each day of therapy. The weighting factors corresponded to the standard errors of the mean of the data on each day to account for the varying degree of certainty between data points. Data and model values were logarithmically transformed to emphasize lower values.
Results
Granulopoiesis in healthy individuals
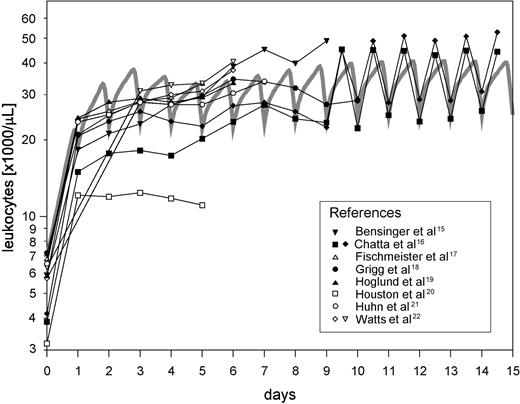
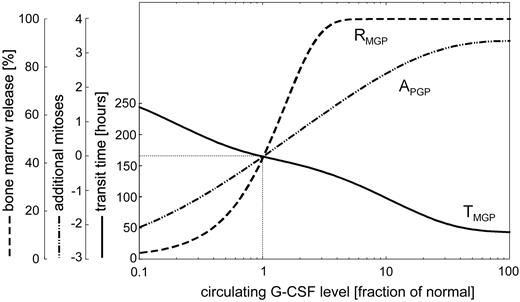
Exogeneous rhG-CSF assistance during conventional chemotherapy usually consists of several consecutive injections once per day at a dose of approximately 5 μg/kg body weight. The effect of such an rhG-CSF scheduling has been studied by several authors in healthy volunteers.15-22 Figure 2 shows these experimental data together with the results of the model simulation. Despite some heterogeneity in the data between the different authors regarding absolute WBC concentrations, the patterns are found to be similar and can be appropriately reproduced by the model. The steepest WBC increase can be observed after the first rhG-CSF injection. This can be explained by the immediate reduction of the transit time in the postmitotic compartment and the increased rate of cells emerging to the peripheral blood. The simulation result also agrees with the daily variation of WBC concentrations observed by Chatta et al, which are caused by the discontinuous mode of rhG-CSF administration. Figure 3 describes the estimated quantitative relationship between the circulating G-CSF level and the 3 assumed G-CSF effects in the model. Under maximum G-CSF stimulation, about 3 additional mitoses take place in the PGP compartment, the transit time in MGP is reduced from a normal value of 165 hours to 43 hours, and the fraction of cells emerging to the blood is increased to 100%.
Effect of repeated daily G-CSF administration in healthy individuals. Good quantitative agreement between model simulation (gray curve) and clinical data (taken from the literature15-22 ).
Effect of repeated daily G-CSF administration in healthy individuals. Good quantitative agreement between model simulation (gray curve) and clinical data (taken from the literature15-22 ).
Dose-response curves for G-CSF effects. Quantitative relationship between the circulating G-CSF level (expressed as fraction of the G-CSF level in the normal steady state) and the 3 modes of G-CSF action. Curve APGP describes the number of additional mitoses at the stage of myeloblasts, promyelocytes, and myelocytes. TMGP describes the transit time in the postmitotic compartment, and RMGP describes the fraction of cells released from bone marrow into peripheral circulation.
Dose-response curves for G-CSF effects. Quantitative relationship between the circulating G-CSF level (expressed as fraction of the G-CSF level in the normal steady state) and the 3 modes of G-CSF action. Curve APGP describes the number of additional mitoses at the stage of myeloblasts, promyelocytes, and myelocytes. TMGP describes the transit time in the postmitotic compartment, and RMGP describes the fraction of cells released from bone marrow into peripheral circulation.
Multicycle chemotherapy
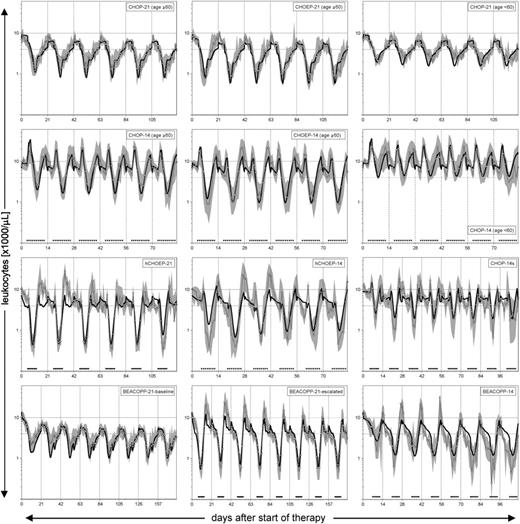
Figure 4 shows the simulation results for the 10 different multicycle chemotherapy regimens together with the WBC data (median and interquartile range) obtained from the clinical trials. Generally, the regimens without rhG-CSF assistance (CHOP-21, CHOEP-21, BEACOPP-21-baseline) exhibit a WBC concentration profile with only one phase of decrease and one consecutive phase of increase per cycle. In contrast, WBC profiles under rhG-CSF–assisted protocols are more complex depending on the time of beginning and cessation of the rhG-CSF injections. Regimens with rhG-CSF initiation at day 4 show a considerable initial increase of WBCs before the chemotherapy-induced decline (CHOP-14, CHOEP-14). This initial increase is much less pronounced in regimens with rhG-CSF initiation at day 6 (CHOP-14s, hCHOEP-14/21) and cannot be observed at all in regimens with injections starting at day 8 (BEACOPP-14, BEACOPP-21-escalated). In all these regimens the WBCs show a decrease after the last rhG-CSF injection.
WBC profiles during chemotherapy with or without rhG-CSF. Model simulation (bold line) compared with clinical trial data (open circles connected by the thin line represent the median WBCs; the gray shaded area depicts the variability by the interquartile range). Dashed vertical lines indicate the start of each therapy cycle. Black triangles indicate the administration of rhG-CSF. The dashed horizontal line marks the normal WBC range.
WBC profiles during chemotherapy with or without rhG-CSF. Model simulation (bold line) compared with clinical trial data (open circles connected by the thin line represent the median WBCs; the gray shaded area depicts the variability by the interquartile range). Dashed vertical lines indicate the start of each therapy cycle. Black triangles indicate the administration of rhG-CSF. The dashed horizontal line marks the normal WBC range.
Comparing CHOEP-21 with CHOP-21 and also CHOEP-14 with CHOP-14, the addition of etoposide leads to noticeably lower nadir counts. Several factors have considerable impact on toxicity, one of which is the age of the patients. This is illustrated by the comparison of CHOP-21 and CHOP-14 for patients younger than 60 years with the same protocols for older patients. No regimen exhibits pronounced cumulative toxicities over successive cycles.
All of these qualitative and quantitative features are reproduced by the model. Although most WBC profiles can be simulated with great accuracy, in some regimens with rhG-CSF assistance (BEACOPP-21-escalated, BEACOPP-14, hCHOEP-21/14) the amplitudes between nadir and peak values are somewhat underestimated in some cycles.
Estimation of drug- and cell stage–specific toxicities
Importantly, the WBC profiles of all regimens can be simulated using a single set of toxicity coefficients as summarized in Table 1. Because the degree of hematotoxicity is age dependent, parameter estimations have been carried out separately for patients younger than 60 and those 60 years or older. Table 1 gives lower and upper boundaries for these estimates. Within these boundaries the agreement between model and data curves did not deviate more than 10% from the optimum as judged by the error function. In most cases, this range is small, which indicates that the values could be estimated with great certainty. However, regarding this 10% tolerance interval, only lower boundaries could be given for kCPH+DOX+VIN and kETO for the PGP compartment and patients 60 years or older, indicating that these parameters are not very sensitive in wide ranges. A major result of the parameter estimation is that the increased toxicity in the elderly can simply be explained by higher toxicity coefficients. Importantly, no differences in other model parameters had to be assumed. Furthermore, the toxicity of all drugs on all cell stages during the first cycle is estimated to be 27% and 31% higher than in later cycles in younger and older patients, respectively.
Estimated toxicity coefficients
Coefficient . | Stem cells/CFU-GM* . | Mitotic precursors† . | Postmitotic precursors‡ . |
|---|---|---|---|
| KCPH + DOX + VIN; 60 or older | 0.195 (0.185-0.198) | 0.5 (> 0.15) | Set to 0.0 |
| kCPH + DOX + VIN; younger than 60 y | 0.178 (0.170-0.185) | 0.098 (0.06-0.1) | Set to 0.0 |
| KETO; 60 y or older | 0.0047 (0.004-0.008) | 0.9496 (> 0.06) | 0.0051 (0.0025-0.008) |
| kETO; younger than 60 y | 0.003 (0.0-0.007) | 0.187 (0.06-0.7) | 0.0019 (0.001-0.0035) |
| KPRO | 0.0063 | 0.0237 | 0.0015 |
| KVIN | 0.0385 | 0.0732 | 0.0 |
| Ffirst-cycle; 60 y or older§ | 1.31 | 1.31 | 1.31 |
| Ffirst-cycle; younger than 60 y§ | 1.27 | 1.27 | 1.27 |
Coefficient . | Stem cells/CFU-GM* . | Mitotic precursors† . | Postmitotic precursors‡ . |
|---|---|---|---|
| KCPH + DOX + VIN; 60 or older | 0.195 (0.185-0.198) | 0.5 (> 0.15) | Set to 0.0 |
| kCPH + DOX + VIN; younger than 60 y | 0.178 (0.170-0.185) | 0.098 (0.06-0.1) | Set to 0.0 |
| KETO; 60 y or older | 0.0047 (0.004-0.008) | 0.9496 (> 0.06) | 0.0051 (0.0025-0.008) |
| kETO; younger than 60 y | 0.003 (0.0-0.007) | 0.187 (0.06-0.7) | 0.0019 (0.001-0.0035) |
| KPRO | 0.0063 | 0.0237 | 0.0015 |
| KVIN | 0.0385 | 0.0732 | 0.0 |
| Ffirst-cycle; 60 y or older§ | 1.31 | 1.31 | 1.31 |
| Ffirst-cycle; younger than 60 y§ | 1.27 | 1.27 | 1.27 |
The values in the parentheses present the limits for the tolerance interval of parameter estimates. See “Results” for further explanation.
S/CG.
PGP.
MGP.
This parameter is assumed to be equal in all compartments.
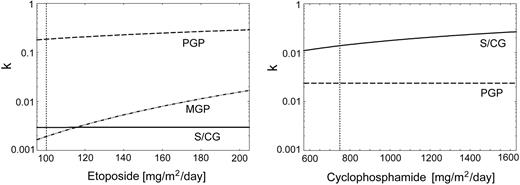
The dose-escalation protocols hCHOEP-14 and hCHOEP-21 were used to estimate the quantitative relationship between drug dosage and toxicity both for etoposide and cyclophosphamide/doxorubicin in patients younger than 60 years (Figure 5). Stem cell toxicity of etoposide is estimated to be considerably lower than for the committed proliferating precursors. Furthermore, there is no dose-toxicity relationship for etoposide on stem cells. The opposite result is obtained for cyclophosphamide, with a higher toxic impact on the stem cell compartment than on the PGP compartment. Also in contrast to etoposide, the toxicity to PGP does not depend on the dose of cyclophosphamide.
Estimated dose-toxicity curves for patients younger than 60 years. The curves show the quantitative relationship between the dose of etoposide and cyclophosphamide and the corresponding toxicity coefficients for the compartments S/CG, PGP, and MGP.
Estimated dose-toxicity curves for patients younger than 60 years. The curves show the quantitative relationship between the dose of etoposide and cyclophosphamide and the corresponding toxicity coefficients for the compartments S/CG, PGP, and MGP.
Model predictions
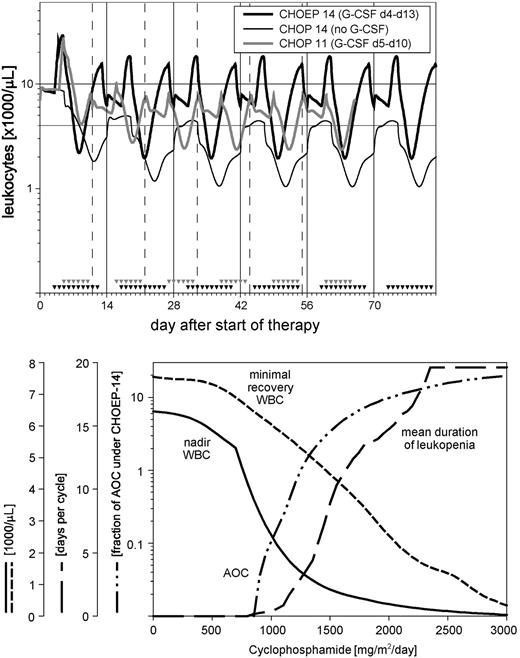
Using the toxicity coefficients and dose-toxicity relationships as shown above, predictive model simulations can be made for variants of the protocols considered here. To enable an appropriate quantitative comparison of different protocol variants, each predicted WBC profile is described by 4 characteristic quantities: (1) the mean duration of leukopenia per therapy cycle (time with WBC below a threshold of 4.0 × 109/L [4000/μL]), (2) the maximum depth of leukopenia during total therapy, (3) the minimum WBC observed at the start of a cycle, and (4) the so-called AOC (area over the simulation curve up to a WBC threshold of 4.0 × 109/L [4000/μL]). A quantitative analysis of the relationship between leukocyte toxicity and the grade of infections based on 2600 cycles of CHOP-21, CHOP-14, CHOEP-21, and CHOEP-14 regimens revealed that the incidence and severity of infections gradually begins to increase below a WBC of 4.0 × 109/L [4000/μL] (data not shown). Table 2 shows the values for these quantities under 4 clinically untested CHOP variants compared with the CHOEP-14 regimen as described in Table 3. One predictive simulation was performed to investigate whether the CHOP-14 protocol can be possibly administered without any rhG-CSF support, because its necessity has not been investigated in any clinical trial so far. In this case the model predicts a toxicity that is more severe than observed under the most intensive CHOEP-14 (WBC profiles in Figure 6). A second predictive model simulation aimed to explore whether an rhG-CSF–assisted CHOP could be further intensified by a reduction of the cycle duration to 11 days. As shown in Table 2 and also in Figure 6, this reduction would lead to a toxicity profile roughly comparable with that observed under rhG-CSF–assisted CHOEP-14. However, a further reduction of the cycle duration to 10 days yields greater toxicities than under CHOEP-14 despite maximum rhG-CSF support from day 2 to day 10. Interestingly, the CHOP-10 variant with less rhG-CSF support (day 4 to day 9) is predicted to be less toxic than the CHOP-10 variant with maximum support.
Model predictions
. | CHOEP-14*; G-CSF days 4 to 13 . | CHOP-14†; no G-CSF . | CHOP-11†; G-CSF days 5 to 10 . | CHOP-10†; G-CSF days 4 to 9 . | CHOP-10†; G-CSF days 2 to 10 . |
|---|---|---|---|---|---|
| Mean duration of neutropenia, d | 2.7 | 9.7 | 2.4 | 3.6 | 4.0 |
| Nadir WBC, × 109/L | 1.9 | 1.0 | 2.4 | 1.5 | 1.4 |
| Minimal recovery, × 109/L | 6.1 | 2.2 | 6.1 | 4.3 | 4.8 |
| AOC, relative to AOC under CHOEP-14 | 1.0 | 5.0 | 0.7 | 1.6 | 2.0 |
. | CHOEP-14*; G-CSF days 4 to 13 . | CHOP-14†; no G-CSF . | CHOP-11†; G-CSF days 5 to 10 . | CHOP-10†; G-CSF days 4 to 9 . | CHOP-10†; G-CSF days 2 to 10 . |
|---|---|---|---|---|---|
| Mean duration of neutropenia, d | 2.7 | 9.7 | 2.4 | 3.6 | 4.0 |
| Nadir WBC, × 109/L | 1.9 | 1.0 | 2.4 | 1.5 | 1.4 |
| Minimal recovery, × 109/L | 6.1 | 2.2 | 6.1 | 4.3 | 4.8 |
| AOC, relative to AOC under CHOEP-14 | 1.0 | 5.0 | 0.7 | 1.6 | 2.0 |
Protocol according to Table 3.
Hypothetical protocol. No clinical data available.
Model predictions for clinically untested chemotherapy regimens. The top panel shows the WBC profile of a hypothetical CHOP-14 without any G-CSF assistance and a hypothetical CHOP-11 compared with CHOEP-14 (as defined in Table 3). The bottom panel shows the quantitative relationship between cyclophosphamide and 4 toxicity measures (see “Results” for further explanation).
Model predictions for clinically untested chemotherapy regimens. The top panel shows the WBC profile of a hypothetical CHOP-14 without any G-CSF assistance and a hypothetical CHOP-11 compared with CHOEP-14 (as defined in Table 3). The bottom panel shows the quantitative relationship between cyclophosphamide and 4 toxicity measures (see “Results” for further explanation).
Figure 6 (lower panel) shows how the toxicity under a CHOP-21 regimen (with rhG-CSF support from day 6 to 13) depends on the dose of cyclophosphamide. The graph allows determination of the maximum tolerable dose of cyclophosphamide for a predefined level of toxicity. For instance, if the WBC concentration at the start of each cycle should not be lower than 4.0 × 109/L (4000/μL), the dose of cyclophosphamide must not exceed 1700 mg/m2/d.
Discussion
In this paper we propose a novel dynamic model of human granulopoiesis for the simulation of the peripheral leukocyte profiles under conventional multidrug multicycle chemotherapies with varying drug composition, dosing, and scheduling. The model also takes into account the effects of concurrent rhG-CSF administration as well as the age-related heterogeneity of hematotoxicity within the patient population. Despite the present restriction of its application to chemotherapy regimens used in lymphoma treatment, the approach is far more general and should be applicable to other regimens as well.
To our knowledge, comparable models allowing such simulations have not yet been published in the literature. Regarding high-dose chemotherapy with autologous stem cell support, which is not addressed here, another mathematical model for granulopoietic reconstitution has recently been proposed by Ostby et al.40
The major result of our work is that a single set of model assumptions and parameters for the main modes of action of cytotoxic drugs and G-CSF could be defined that consistently explains the peripheral WBC profiles observed in 10 different chemotherapies. Importantly, most of these model assumptions and some parameter estimates are well supported by direct or indirect experimental evidence. It is widely accepted that G-CSF–induced neutrophilia mainly originates from a combination of 2 cell kinetic mechanisms: an enhanced mitotic activity at immature proliferative cell stages and an accelerated transit through the postmitotic pool.41-43 Price et al determined granuloid precursor pool sizes and postmitotic pool transit times in healthy human beings following daily stimulation with 300 μg rhG-CSF. Given the quantitative relationship between the G-CSF level and the number of additional mitoses in the proliferative precursor compartment (Figure 3), the relative increases of mitotic precursor numbers found in this experimental investigation agree well with our model results. The minimum postmitotic transit time of 43 hours estimated by our model, however, is somewhat lower than obtained by Price (approximately 70 hours). This discrepancy can be explained by the fact that this minimal transit time is only reached at maximum circulating G-CSF concentrations shortly after subcutaneous G-CSF injection. Due to the rapid elimination of G-CSF from circulation within a few hours, the mean transit time over 24 hours may be considerably higher. However, the 2 cell kinetic mechanisms mentioned above do not sufficiently explain the sustained elevation of peripheral granulocytes during G-CSF stimulation. More detailed model investigations in the mouse system have suggested that a third mechanism is likely to be involved.44 This is addressed as a G-CSF–dependent survival factor of mature granulocytes. In our human model we therefore assumed that under normal steady state conditions only a certain fraction of postmitotic neutrophil precursors emerges from the bone marrow into the circulation. This fraction is estimated to be approximately 43% and can be increased to 100% under maximum G-CSF stimulation. Independent confirmation on this mechanism was recently provided by Mackey et al, who measured the apoptotic rate of postmitotic neutrophil precursors in 12 healthy human beings and found that about 55% of the cells entering this compartment die before being released into the blood.45
Several experimental and clinical investigations have suggested that G-CSF is removed from circulation both by nonspecific renal elimination and an active receptor-mediated clearance process.29,46,47 The G-CSF clearance has been shown to increase with the total mass of available receptors, which mainly depends on the number of mature neutrophils bearing these receptors. The assumption of such a specific elimination process in the model leads to G-CSF serum level dynamics that are in close agreement to pharmacokinetic measurements of Borleffs et al obtained in healthy subjects48 (results not shown). Recently, a new polyethylene glycol conjugated filgrastim derivative (pegfilgrastim) has been developed with a markedly sustained duration of activity as compared with normal rhG-CSF. The pharmacokinetic and pharmacodynamic properties of this new drug will be considered in a next development step of our model.
The proposed model does only consider the neutrophilic lineage. However, parameter estimations and model predictions are based on leukocyte counts because data on neutrophil numbers were not available from the clinical trials. Using correlation and linear regression analysis, different authors have demonstrated a close linear relationship between the leukocyte and neutrophil count under myelosuppressive chemotherapy.49-51 These findings suggest that only minor error should be introduced by referring to WBCs instead to neutrophil counts.
Our model results could be obtained on the basis of simplifying assumptions about the damaging effects of the cytostatic drugs. First, it was not necessary to assume interactions between the toxicity coefficients. All model results were obtained assuming an additive (ie, independent) effect of each drug. This is supported by the fact that the drugs considered here all have different molecular modes of action and targets. Second, the cytocidal drug effect starts immediately after administration, lasts only for a short period of 24 hours, and is proportional to the number of target cells, hence leading to the concept of toxicity coefficients. This qualitative feature agrees well with the dynamic patterns of cell depletion and recovery particularly observed in the proliferative bone marrow stages after single bolus drug administrations. Such experimental studies have extensively been reviewed by Lohrmann and Schreml.52 Furthermore, neither delayed nor prolonged drug effects had to be assumed. Thus, the dynamic behavior of the granulopoietic system after the short-term damage primarily depends on the cell kinetic and regulatory properties that are unaffected by the cytotoxic drugs. However, the transit time values were crucial with regard to the nadir time points in our simulations. These parameters have in fact been determined in former model analyses of human cyclical neutropenia by our group and now shown to be also appropriate in the present simulations.25,27
A major result of parameter estimation was the finding that the magnitudes of toxic effects for the compartments S/CG and the committed precursor cell compartment PGP were different. The parameter estimates obtained after fitting of the model to the data suggested a higher toxicity of cyclophosphamide and doxorubicin for the stem cell compartment than for the later stages. Interestingly, this relationship was reversed for etoposide. These qualitative findings are supported by experimental studies.52 However, no distinction between the toxicities in S and its immediate successor CG was necessary. A somewhat higher toxicity of the cytoreductive therapy had to be assumed during the first treatment course. Without this assumption all model simulations yielded a less pronounced leukopenia during the first cycle as compared with the following cycles. This difference results from the fact that the first cycle is applied when the system is in a normal steady state, but all other cycles are applied when the system has not fully recovered from the perturbation caused by the preceding cycle. However, this phenomenon could not be observed in the clinical data, which might be the expression of a somewhat higher sensitivity of the cells to the damage.
In the present work we only analyzed the average leukocyte profile in a population subjected to defined chemotherapy. It is, however, well known that hematotoxicity shows large interindividual heterogeneity despite homogeneous dose delivery. One factor related to the extent of toxic response to chemotherapy is the age of the patients. Older patients usually show more excessive hematotoxicity than younger patients. An important model finding is that this difference can be explained by a different toxic responsiveness (ie, different toxicity coefficients) rather than differences in the cell kinetic or regulatory parameters. This agrees with experimental studies in which no age-related differences in the proportion of CD34+ marrow cells, bone marrow neutrophil reserves, or peripheral neutrophil counts could be found.53,54 Although a reduced proliferative responsiveness of early precursors to G-CSF has been observed in vitro, no relevant difference in the effect of exogenous rhG-CSF administration seems to exist between young and elderly subjects.55 Arefined model analysis of the interindividual heterogeneity of hematotoxicity is in progress.
Moderate dose escalation or intensification of conventional chemotherapy has recently proven to be effective in the treatment of malignant lymphomas1-3 and may also be a successful strategy to improve the outcome in other tumor entities. For the design of an appropriate dose intensified regimen, 2 major competing aspects have to be considered, the expected therapeutic benefit on the one hand and the feasibility of the regimen (toxicity, maintenance of dose intensity) on the other hand. Regarding the former aspect it has been shown that a model-based inference from the dosing and timing of cytostatic drugs on the therapeutic effectiveness is possible. The dose-intensified BEACOPP regimens of the German Hodgkin's Lymphoma Study Group have been developed on the basis of such a tumor growth model, which allowed estimation of the effective dose-outcome relationship and the relative potency of cytostatic drugs.56,57 As far as chemotherapy feasibility is concerned, the preclinical selection of appropriate regimens might be facilitated by the model proposed here. It must be emphazised, however, that our model cannot be used for risk assessment for infectious complications resulting from neutropenia because sound quantitative data on the relationship between the dynamics of neutropenia and the infections are largely lacking. However, the present model can be used to make predictions on toxic effects of protocol variants that have not yet been clinically tested and compare these with the toxicity profiles of related protocols already tested.
The model proposed here has been developed on the basis of regimens used in the treatment of malignant lymphomas. Nonetheless, the model concept and the assumptions on the effects of cytotoxic drugs and G-CSF are also applicable to regimens used for the treatment of other tumor entities provided that the drug effects can be estimated from appropriate trial data as illustrated above.
Prepublished online as Blood First Edition Paper, June 29, 2004; DOI 10.1182/blood-2004-01-0306.
Supported by the Deutsche Forschungsgemeinschaft (DFG), Bonn, Germany, grant no. LO 342/8-2 (M.L.).
The publication costs of this article were defrayed in part by page charge payment. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 U.S.C. section 1734.
This paper is dedicated to our friend and colleague Horst Franke, whose death took us all by surprise. We are indebted to him for the many years of fruitful collaboration and committed discussions. We thank the German Hodgkin's Lymphoma Study Group (Volker Diehl, chairman) and the German High-Grade Non-Hodgkin's Lymphoma Study Group (Michael Pfreundschuh, chairman) for the kind permission to use the clinical trial data.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal