We have read with interest the paper by Press et al1 that reported a phase I/II trial of iodine-131-tositumomab in combination with etoposide, cyclophosphamide, and autologous stem cell transplantation for relapsing B-cell lymphomas.
Objectives, design, and analysis of the trial are very accurately reported, as well as the data (with the actual doses and toxicities of all 52 treated patients). The main objective of the trial was to estimate the maximum tolerated dose (MTD) of iodine-131-tositumomab, defined as the dose associated with a 25% toxic rate. Design and analysis of the trial were based on a grouped up-and-down scheme, using cohorts of 4 patients. The principal advantage of this method is its simplicity and its great ease of application. But we have some ethical and statistical concerns with the use of such a design in evaluating the MTD.
First, the observed toxic rate associated with the estimated MTD was 0.174 (4 of 23), as reported in Table 3. But such a statistical conclusion involves uncertainty. It should have been informative to give an estimate of the 95% confidence interval of the toxic rate associated with MTD, which can be exactly computed from the paper results at [0.05-0.388]. In addition, the estimated MTD was empirically defined by the dose received by 20 patients (ie, 5 cohorts), provided that the lower limit of the 80% one-sided confidence interval associated with the observed toxicity rate did not exceed the 25% target toxicity rate. This latter statistical restriction should be more clearly explained and justified.
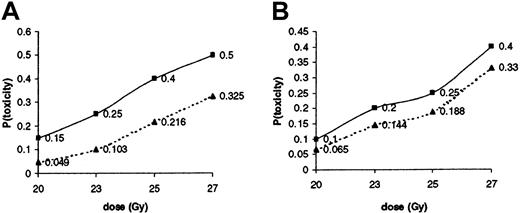
Second, these up-and-down designs poorly address ethical concerns (such as minimal sample size) that have become a major issue in the conduct and analysis of dose-ranging phase I oncology trials. Several new approaches have been introduced that more explicitly address these concerns. They are usually derived from the continual reassessment method (CRM), a sequential Bayesian approach that allows, in defining the dose to be administered to the next patient (or the next cohort of patients), for incorporating evidence from previous experience and previous experiments jointly with information accumulated along the trial.2 Patients are entered sequentially, and the toxic probability associated with each dose level is updated, using Bayes formula together with the available information on doses and observed toxicities. Each patient of the next cohort is then treated at the dose level for which the updated toxicity rate is closest to the target (here, 25%). It facilitates a commonsense interpretation of statistical conclusions by allowing for direct probability statements, such as the probability that the toxic rate of a dose level is in some interval around the target. Moreover, this Bayesian (probability) interval for an unknown toxic rate can be regarded as having high probability of containing the unknown quantity, in contrast to a confidence interval, which may strictly be interpreted only in relation to a sequence of similar inferences that might be made in repeated practice. Additionally, Bayesian approach enables calculations of probabilities of future observations, from which several stopping rules can be derived, allowing an easy and reproducible decision either to continue patient accrual or to stop inclusions.3 We have retrospectively applied the CRM to the available data on the 47 patients who were actually administered the tositumomab. Using either 23 Gy (dose 2) or 25 Gy (dose 3) as the initial guess of MTD (as required by the Bayesian paradigm), we found from the updated dose-toxicity relationship that 25 Gy was the estimate of the MTD, with posterior toxic rate associated with MTD at 0.216 (95% Bayesian interval: [0.108-0.352], Figure 1A) or 0.188 ([0.089-0.316], Figure 1B), respectively. Our findings confirm the results of Press et al. Nevertheless, the sequential computation after each cohort of 4 patients of stopping rules based on the predictive distribution of the number of toxicities observed in the next 4 patients would have yielded to an earlier stopping of the accrual, at most after 36 patients.
Updating of the initial guess of dose-toxicity relationship after enrollment of 47 patients.
Data available on the 47 treated patients were modeled using CRM. The results are presented as the initial guesses (▪) of probability of toxicity at each dose level, updated (▴) after enrollment of 47 patients, using either 23 Gy (A) or 25 Gy (B) as the initial candidate for MTD. Modeling used a 1-parameter logistic model with the scale parameter fixed at 3 and a unit exponential prior for the shape parameter.
Updating of the initial guess of dose-toxicity relationship after enrollment of 47 patients.
Data available on the 47 treated patients were modeled using CRM. The results are presented as the initial guesses (▪) of probability of toxicity at each dose level, updated (▴) after enrollment of 47 patients, using either 23 Gy (A) or 25 Gy (B) as the initial candidate for MTD. Modeling used a 1-parameter logistic model with the scale parameter fixed at 3 and a unit exponential prior for the shape parameter.
We conclude that sequential Bayesian approaches may provide useful information on the dose-toxicity relationship so that its use in planning further phase I/II trials should be encouraged among investigators in hematology, as it has been done in other fields.4
Statistical designs for clinical trials of radioimmunotherapy
We agree with Vincent Levy et al that there are “newer” designs for dose-finding studies that may prove preferable to the more standard designs that are commonly employed, particularly when the more standard designs define an MTD with as few as 3 to 6 patients. In fact, we have ongoing dose-finding studies that utilize these alternate designs. But we believe that the design that was employed in the phase I/II trial of iodine-131-tositumomab in combination with etoposide, cyclophosphamide, and autologous stem cell transplantation for relapsing B-cell lymphomas that we reported had operating characteristics that were more than acceptable, and this provided us with sufficient confidence to implement this design in practice.
Levy et al point out that the observed toxicity rate at the estimated MTD involved uncertainty and that confidence intervals should have been provided. Any estimate of an MTD will involve uncertainty, of course, regardless of the method used. We chose not to provide estimates of a confidence interval, however, as the observed toxicity rate at the defined MTD would be biased since the dose-finding rules restrict what could be observed in order to deem a dose as the MTD. The restriction of requiring the MTD to have an associated lower limit to the corresponding one-sided 80% confidence interval that does not exceed 25% was largely based on heuristic grounds. Nonetheless, this rule led to operating characteristics that were more than adequate for a wide range of assumed-true dose-response relationships. The greater precision of the Bayesian confidence intervals reflects to a large extent the information that has been added to the statistical model through the choice of an initial guess at the MTD and a prior distribution, even before any data have been collected. Whether this is a strength or weakness of the Bayesian approach is a continuing philosophical debate that need not be addressed here.

This feature is available to Subscribers Only
Sign In or Create an Account Close Modal